Advertisements
Advertisements
प्रश्न
If Young's double slit experiment is performed in water, _________________ .
विकल्प
the fringe width will decrease
the fringe width will increase
the fringe width will remain unchanged
there will be no fringe
उत्तर
the fringe width will decrease
As fringe width is proportional to the wavelength and wavelength of light is inversely proportional to the refractive index of the medium,
Here,
\[\lambda_M = \lambda/\eta\]
\[ \lambda_M = \text{wavelength in medium}\]
\[\lambda = \text{wavelength in vacuum}\]
\[\eta = \text{refractive index of medium}\]
Hence, fringe width decreases when Young's double slit experiment is performed under water.
APPEARS IN
संबंधित प्रश्न
Show that the fringe pattern on the screen is actually a superposition of slit diffraction from each slit.
In a double-slit experiment the angular width of a fringe is found to be 0.2° on a screen placed 1 m away. The wavelength of light used is 600 nm. What will be the angular width of the fringe if the entire experimental apparatus is immersed in water? Take refractive index of water to be 4/3.
Using analytical method for interference bands, obtain an expression for path difference between two light waves.
A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young's double slit experiment with fringe width 0.5 mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit.
Write three characteristic features to distinguish between the interference fringes in Young's double slit experiment and the diffraction pattern obtained due to a narrow single slit.
How does the fringe width get affected, if the entire experimental apparatus of Young is immersed in water?
The slits in a Young's double slit experiment have equal width and the source is placed symmetrically with respect to the slits. The intensity at the central fringe is I0. If one of the slits is closed, the intensity at this point will be ____________ .
The separation between the consecutive dark fringes in a Young's double slit experiment is 1.0 mm. The screen is placed at a distance of 2.5m from the slits and the separation between the slits is 1.0 mm. Calculate the wavelength of light used for the experiment.
In a Young's double slit experiment, using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 micron (1 micron = 10−6 m) is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the screen and the slits is doubled. It is found that the distance between the successive maxima now is the same as the observed fringe-shift upon the introduction of the mica sheet. Calculate the wavelength of the monochromatic light used in the experiment.
Two transparent slabs having equal thickness but different refractive indices µ1 and µ2are pasted side by side to form a composite slab. This slab is placed just after the double slit in a Young's experiment so that the light from one slit goes through one material and the light from the other slit goes through the other material. What should be the minimum thickness of the slab so that there is a minimum at the point P0 which is equidistant from the slits?
A double slit S1 − S2 is illuminated by a coherent light of wavelength \[\lambda.\] The slits are separated by a distance d. A plane mirror is placed in front of the double slit at a distance D1 from it and a screen ∑ is placed behind the double slit at a distance D2 from it (see the following figure). The screen ∑ receives only the light reflected by the mirror. Find the fringe-width of the interference pattern on the screen.
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of diameter of the ring. The ring will now rotate with an angular velocity:
An unpolarised beam of intensity 2a2 passes through a thin polaroid. Assuming zero absorption in the polaroid, the intensity of emergent plane polarised light will be
In Young's double slit experiment, the minimum amplitude is obtained when the phase difference of super-imposing waves is: (where n = 1, 2, 3, ...)
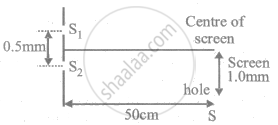
In Young's double slit experiment shown in figure S1 and S2 are coherent sources and S is the screen having a hole at a point 1.0 mm away from the central line. White light (400 to 700 nm) is sent through the slits. Which wavelength passing through the hole has strong intensity?
ASSERTION (A): In an interference pattern observed in Young's double slit experiment, if the separation (d) between coherent sources as well as the distance (D) of the screen from the coherent sources both are reduced to 1/3rd, then new fringe width remains the same.
REASON (R): Fringe width is proportional to (d/D).
How will the interference pattern in Young's double-slit experiment be affected if the screen is moved away from the plane of the slits?
A fringe width of 6 mm was produced for two slits separated by 1 mm apart. The screen is placed 10 m away. The wavelength of light used is 'x' nm. The value of 'x' to the nearest integer is ______.
The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is ______.
In Young's double-slit experiment, the separation between the two slits is d and the distance of the screen from the slits is 1000 d. If the first minima fall at a distance d from the central maximum, obtain the relation between d and λ.
