Advertisements
Advertisements
प्रश्न
The line-width of a bright fringe is sometimes defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum. Find the line-width of a bright fringe in a Young's double slit experiment in terms of \[\lambda,\] d and D where the symbols have their usual meanings.
उत्तर
Given:-
Separation between two slits = d
Wavelength of the light = \[\lambda\]
Distance of the screen = D
Let Imax be the maximum intensity and I be half the maximum intensity at a point at a distance y from the central point.
So, \[I = a^2 + a^2 + 2 a^2 \cos\phi\]
Here, \[\phi\] is the phase difference in the waves coming from the two slits.
So, \[I = 4 a^2 \cos^2 \left( \frac{\phi}{2} \right)\]
\[\Rightarrow \frac{I}{I_\max} = \frac{1}{2}\]
\[ \Rightarrow \frac{4 a^2 \cos^2 \left( \frac{\phi}{2} \right)}{4 a^2} = \frac{1}{2}\]
\[ \Rightarrow \cos^2 \left( \frac{\phi}{2} \right) = \frac{1}{2}\]
\[ \Rightarrow \cos\left( \frac{\phi}{2} \right) = \frac{1}{\sqrt{2}}\]
\[ \Rightarrow \frac{\phi}{2} = \frac{\pi}{4}\]
\[ \Rightarrow \phi = \frac{\pi}{2}\]
Corrosponding path difference, \[∆ x = \frac{1}{4}\]
\[ \Rightarrow y = \frac{∆ xD}{d} = \frac{\lambda D}{4d}\]
The line-width of a bright fringe is defined as the separation between the points on the two sides of the central line where the intensity falls to half the maximum.
So, line-width = 2y
\[= 2\frac{D\lambda}{4d} = \frac{D\lambda}{2d}\]
Thus, the required line width of the bright fringe is \[\frac{D\lambda}{2d}.\]
APPEARS IN
संबंधित प्रश्न
In Young's double slit experiment, describe briefly how bright and dark fringes are obtained on the screen kept in front of a double slit. Hence obtain the expression for the fringe width.
Using monochromatic light of wavelength λ in Young’s double slit experiment, the eleventh dark fringe is obtained on the screen for a phase difference of ______.
Using analytical method for interference bands, obtain an expression for path difference between two light waves.
Explain two features to distinguish between the interference pattern in Young's double slit experiment with the diffraction pattern obtained due to a single slit.
A monochromatic light of wavelength 500 nm is incident normally on a single slit of width 0.2 mm to produce a diffraction pattern. Find the angular width of the central maximum obtained on the screen.
Estimate the number of fringes obtained in Young's double slit experiment with fringe width 0.5 mm, which can be accommodated within the region of total angular spread of the central maximum due to single slit.
In Young’s double slit experiment, show graphically how the intensity of light varies with distance
In Young's double slit experiment, derive the condition for
(i) constructive interference and
(ii) destructive interference at a point on the screen.
If the separation between the slits in a Young's double slit experiment is increased, what happens to the fringe-width? If the separation is increased too much, will the fringe pattern remain detectable?
If the source of light used in a Young's double slit experiment is changed from red to violet, ___________ .
A plate of thickness t made of a material of refractive index µ is placed in front of one of the slits in a double slit experiment. (a) Find the change in the optical path due to introduction of the plate. (b) What should be the minimum thickness t which will make the intensity at the centre of the fringe pattern zero? Wavelength of the light used is \[\lambda.\] Neglect any absorption of light in the plate.
A transparent paper (refractive index = 1.45) of thickness 0.02 mm is pasted on one of the slits of a Young's double slit experiment which uses monochromatic light of wavelength 620 nm. How many fringes will cross through the centre if the paper is removed?
How is the fringe width of an interference pattern in Young's double-slit experiment affected if the two slits are brought closer to each other?
In Young's double-slit experiment, the two slits are separated by a distance of 1.5 mm, and the screen is placed 1 m away from the plane of the slits. A beam of light consisting of two wavelengths of 650 nm and 520 nm is used to obtain interference fringes.
Find the distance of the third bright fringe for λ = 520 nm on the screen from the central maximum.
In Young’s double slit experiment, what is the effect on fringe pattern if the slits are brought closer to each other?
A thin circular ring of mass M and radius R is rotating about its axis with a constant angular velocity ω. Two objects each of mass m are attached gently to the opposite ends of diameter of the ring. The ring will now rotate with an angular velocity:
A projectile can have the same range R for two angles of projection. If t1 and t2 be the times of flight in two cases, then what is the product of two times of flight?
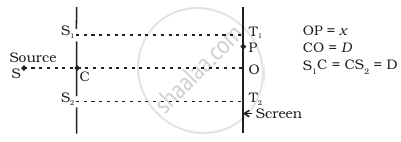
Consider a two-slit interference arrangement (Figure) such that the distance of the screen from the slits is half the distance between the slits. Obtain the value of D in terms of λ such that the first minima on the screen falls at a distance D from the centre O.
The maximum number of possible interference maxima for slit-separation equal to twice the wavelength in Young's double-slit experiment is ______.
- Assertion (A): In Young's double slit experiment all fringes are of equal width.
- Reason (R): The fringe width depends upon the wavelength of light (λ) used, the distance of the screen from the plane of slits (D) and slits separation (d).
