Advertisements
Advertisements
Question
A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
If the triangle ABC in the above question is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained.
Solution
(i)
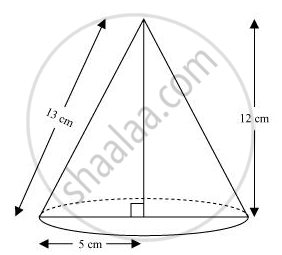
When right-angled ΔABC is revolved about its side 12 cm, a cone with height (h) as 12 cm, radius (r) as 5 cm, and slant height (l) 13 cm will be formed.
Volume of cone = `1/3πr^2h`
= `[1/3xx pi xx(5)^2xx12]cm^3`
= 100π cm3
Therefore, the volume of the cone so formed is 100π cm3.
(ii)
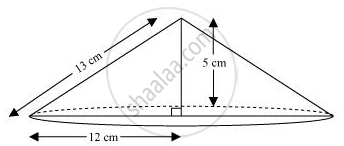
When right-angled ΔABC is revolved about its side 5 cm, a cone will be formed having radius (r) as 12 cm, height (h) as 5 cm, and slant height (l) as 13 cm.
Volume of cone = `1/3pir^2h`
= `[1/3xx pi xx(12)^2xx5]cm^3`
= 240π cm3
Therefore, the volume of the cone so formed is 240π cm3.
Required ratio = `(100pi)/(240pi) = 5/12 = 5 : 12`.
APPEARS IN
RELATED QUESTIONS
Find the capacity in litres of a conical vessel with height 12 cm and slant height 13 cm.
`["Assume "pi=22/7]`
If the height and slant height of a cone are 21 cm and 28 cm respectively. Find its volume.
The total surface area of a cone of radius `r/2` and length 2l, is
The curved surface area of one cone is twice that of the other while the slant height of the latter is twice that of the former. The ratio of their radii is
The ratio of the volume of a right circular cylinder and a right circular cone of the same base and height, is
The diameters of two cones are equal. If their slant heights are in the ratio 5 : 4, the ratio of their curved surface areas, is
The height of a solid cone is 12 cm and the area of the circular base is 64 `pi`cm2. A plane parallel to the base of the cone cuts through the cone 9 cm above the vertex of the cone, the areas of the base of the new cone so formed is
If a cone is cut into two parts by a horizontal plane passing through the mid-point of its axis, the axis, the ratio of the volumes of upper and lower part is
There are 25 persons in a tent which is conical in shape. Every person needs an area of 4 sq.m. of the ground inside the tent. If height of the tent is 18 m, find the volume of the tent.
If the ratio of radius of base and height of a cone is 5:12 and its volume is 314 cubic metre. Find its perpendicular height and slant height. (π = 3.14)
