Advertisements
Advertisements
प्रश्न
A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
If the triangle ABC in the above question is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained.
उत्तर
(i)
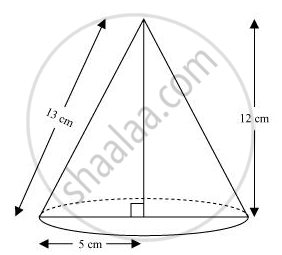
When right-angled ΔABC is revolved about its side 12 cm, a cone with height (h) as 12 cm, radius (r) as 5 cm, and slant height (l) 13 cm will be formed.
Volume of cone = `1/3πr^2h`
= `[1/3xx pi xx(5)^2xx12]cm^3`
= 100π cm3
Therefore, the volume of the cone so formed is 100π cm3.
(ii)
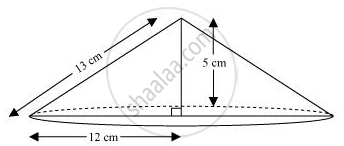
When right-angled ΔABC is revolved about its side 5 cm, a cone will be formed having radius (r) as 12 cm, height (h) as 5 cm, and slant height (l) as 13 cm.
Volume of cone = `1/3pir^2h`
= `[1/3xx pi xx(12)^2xx5]cm^3`
= 240π cm3
Therefore, the volume of the cone so formed is 240π cm3.
Required ratio = `(100pi)/(240pi) = 5/12 = 5 : 12`.
APPEARS IN
संबंधित प्रश्न
Find the volume of the right circular cone with radius 3.5 cm and height 12 cm.
`["Assume "pi=22/7]`
Find the capacity in litres of a conical vessel with radius 7 cm and slant height 25 cm.
`["Assume "pi=22/7]`
The height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of its base. [Use π = 3.14]
The height of a cone is 15 cm. If its volume is 500 π cm3, then find the radius of its base.
If the height and slant height of a cone are 21 cm and 28 cm respectively. Find its volume.
Mark the correct alternative in each of the following:
The number of surfaces of a cone has, is
The total surface area of a cone of radius `r/2` and length 2l, is
If h, S and V denote respectively the height, curved surface area and volume of a right circular cone, then `3 pi Vh^3 - S^2h^2 + 9V^2` is equal to
Volume of a cone is 6280 cubic cm and base radius of the cone is 20 cm. Find its perpendicular height. (π = 3.14)
In a field, dry fodder for the cattle is heaped in a conical shape. The height of the cone is 2.1m. and diameter of base is 7.2 m. Find the volume of the fodder. if it is to be covered by polythin in rainy season then how much minimum polythin sheet is needed ?
`( π = 22/7 ) and sqrt 17.37 = 4.17`
