Advertisements
Advertisements
Question
A solid sphere rolls down two different inclined planes of the same heights but different angles of inclination. (a) Will it reach the bottom with the same speed in each case? (b) Will it take longer to roll down one plane than the other? (c) If so, which one and why?
Solution 1
(a) Yes (b) Yes (c) On the smaller inclination
(a)Mass of the sphere = m
Height of the plane = h
Velocity of the sphere at the bottom of the plane = v
At the top of the plane, the total energy of the sphere = Potential energy = mgh
At the bottom of the plane, the sphere has both translational and rotational kinetic energies.
Hence, total energy = `1/2mv^2 + 1/2Iomega^2`
Using the law of conservation of energy, we can write:
`1/2mv^2 + 1/2 Iomega^2 = mgh` ....(I)
For a solid sphere, the moment of inertia about its centre, `I = 2/3 mr^2`
Hence, equation (i) becomes:
`1/2 mv^2 + 1/2 (2/5 mr^2)omega^2 = mgh`
`1/2v^2 + 1/5r^2omega^2 =gh`
But we have the relation `v= r omega`
`:.1/2v^2 + 1/5v^2 = gh`
`v^2(7/10) = gh`
`v = sqrt(10/7 gh)`
Hence, the velocity of the sphere at the bottom depends only on height (h) and acceleration due to gravity (g). Both these values are constants. Therefore, the velocity at the bottom remains the same from whichever inclined plane the sphere is rolled.
(b), (c)Consider two inclined planes with inclinations θ1 and θ2, related as: θ1 < θ2
The acceleration produced in the sphere when it rolls down the plane inclined at `theta_1` is g sin `theta_1`
The various forces acting on the sphere are shown in the following figure.
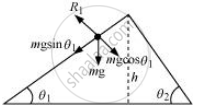
R1 is the normal reaction to the sphere.
Similarly, the acceleration produced in the sphere when it rolls down the plane inclined at θ2is:
g sin θ2
The various forces acting on the sphere are shown in the following figure.
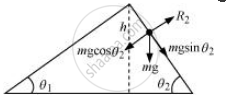
R2 is the normal reaction to the sphere.
θ2 > θ1; sin θ2 > sin θ1 ... (i)
∴ a2 > a1 … (ii)
Initial velocity, u = 0
Final velocity, v = Constant
Using the first equation of motion, we can obtain the time of roll as:
v = u + at
`:. t prop 1/a`
`[("For inclination" theta_1: t_1 prop 1/a_1), ("For inclination" theta_2 : t_2 prop 1/a_2)]` ...(iii)
From equations (ii) and (iii), we get:
t2 < t1
Hence, the sphere will take a longer time to reach the bottom of the inclined plane having the smaller inclination
Solution 2
(a) Using law of conservation of energy,
`1/2mv^2 + 1/2Iomega^2 = mgh`
or `1/2mv^2 + 1/2(2/5 mR^2) v^2/R^2 = mgh`
or 7/10v^2 = gh or v = `sqrt((10gh)/7)`
Since h is same for both the inclined planes therefore v is the same.
b) `l = 1/2((g sin theta)/(1+K^2/R^2)) t^2 = (g sin theta)/2(1+2/5) t^2 = (5g sin theta)/14 t^2`
or t = `sqrt((14l)/(5g sin theta)`
Now, `sin theta = h/l` or l = `h/sin theta`
`:. t= 1/sin theta sqrt((14h)/"5g")`
Lesser the value of `theta` more will be t
c) Clearly, the solid sphere will take longer to roll down the plane with smaller inclination.
APPEARS IN
RELATED QUESTIONS
Read each statement below carefully, and state, with reasons, if it is true or false;
The instantaneous speed of the point of contact during rolling is zero.
A cylinder rolls on a horizontal place surface. If the speed of the centre is 25 m/s, what is the speed of the highest point?
A string is wrapped over the edge of a uniform disc and the free end is fixed with the ceiling. The disc moves down, unwinding the string. Find the downward acceleration of the disc.
The speed of a solid sphere after rolling down from rest without sliding on an inclined plane of vertical height h is, ______
A solid sphere rolls down from top of inclined plane, 7m high, without slipping. Its linear speed at the foot of plane is ______. (g = 10 m/s2)
The power (P) is supplied to rotating body having moment of inertia 'I' and angular acceleration 'α'. Its instantaneous angular velocity is ______.
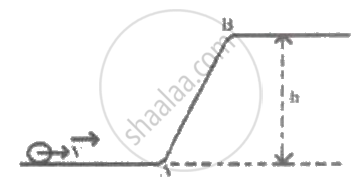
A solid sphere is rolling on a frictionless surface with translational velocity 'V'. It climbs the inclined plane from 'A' to 'B' and then moves away from Bon the smooth horizontal surface. The value of 'V' should be ______.
The angular velocity of minute hand of a clock in degree per second is ______.
The angular displacement of a particle in 6 sec on a circle with angular velocity `pi/3` rad/sec is ______.
A disc of mass 4 kg rolls on a horizontal surface. If its linear speed is 3 m/ s, what is its total kinetic energy?
