Advertisements
Advertisements
Question
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to be done to stop it?
Solution 1
Radius of the hoop, r = 2 m
Mass of the hoop, m = 100 kg
Velocity of the hoop, v = 20 cm/s = 0.2 m/s
Total energy of the hoop = Translational KE + Rotational KE
`E_r = 1/2mv^2 + 1/2 Iomega^2`
Moment of inertia of the hoop about its centre, I = mr2
`E_r = 1/2 mv^2 + 1/2(mr^2)omega^2`
But we have the relation, `v = romega`
`:.E_r = 1/2 mv^2 + 1/2 mr^2omega^2`
`=1/2mv^2 + 1/2 mv^2 = mv^2`
The work required to be done for stopping the hoop is equal to the total energy of the hoop.
∴Required work to be done, W = mv2 = 100 × (0.2)2 = 4 J
Solution 2
Here, R = 2 m, M = 100 kg
v = 20 cm/s = 0.2 m/s
Total energy of the hoop =1/2Mv2 + 1/2Iw2
=1/2Mv2 + 1/2(MR2)w2
=1/2Mv2 +1/2Mv2 =Mv2
Work required to stop the hoop = total energy of the hoop W = Mv2 = 100 (0.2)2= 4 Joule
APPEARS IN
RELATED QUESTIONS
Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.
(Hint: The moment of inertia of the door about the vertical axis at one end is ML2/3.)
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not.
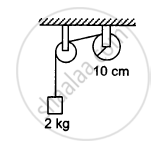
A string is wrapped on a wheel of moment of inertia 0⋅20 kg-m2 and radius 10 cm and goes through a light pulley to support a block of mass 2⋅0 kg as shown in the following figure. Find the acceleration of the block.
A kid of mass M stands at the edge of a platform of radius R which can be freely rotated about its axis. The moment of inertia of the platform is I. The system is at rest when a friend throws a ball of mass m and the kid catches it. If the velocity of the ball is \[\nu\] horizontally along the tangent to the edge of the platform when it was caught by the kid, find the angular speed of the platform after the event.
Two blocks of masses 400 g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has a moment of inertia \[1 \cdot 6 \times {10}^{- 4} kg - m^2\] and a radius 2⋅0 cm, Find (a) the kinetic energy of the system as the 400 g block falls through 50 cm, (b) the speed of the blocks at this instant.
From a circular ring of mass ‘M’ and radius ‘R’ an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR2 ’. Then the value of ‘K’ is ______.
Why does a solid sphere have smaller moment of inertia than a hollow cylinder of same mass and radius, about an axis passing through their axes of symmetry?
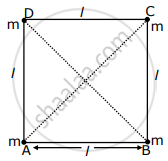
Four equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be ______.