Advertisements
Advertisements
प्रश्न
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to be done to stop it?
उत्तर १
Radius of the hoop, r = 2 m
Mass of the hoop, m = 100 kg
Velocity of the hoop, v = 20 cm/s = 0.2 m/s
Total energy of the hoop = Translational KE + Rotational KE
`E_r = 1/2mv^2 + 1/2 Iomega^2`
Moment of inertia of the hoop about its centre, I = mr2
`E_r = 1/2 mv^2 + 1/2(mr^2)omega^2`
But we have the relation, `v = romega`
`:.E_r = 1/2 mv^2 + 1/2 mr^2omega^2`
`=1/2mv^2 + 1/2 mv^2 = mv^2`
The work required to be done for stopping the hoop is equal to the total energy of the hoop.
∴Required work to be done, W = mv2 = 100 × (0.2)2 = 4 J
उत्तर २
Here, R = 2 m, M = 100 kg
v = 20 cm/s = 0.2 m/s
Total energy of the hoop =1/2Mv2 + 1/2Iw2
=1/2Mv2 + 1/2(MR2)w2
=1/2Mv2 +1/2Mv2 =Mv2
Work required to stop the hoop = total energy of the hoop W = Mv2 = 100 (0.2)2= 4 Joule
APPEARS IN
संबंधित प्रश्न
Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction µs = 0.25.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not.
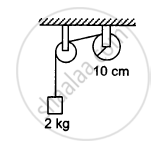
A string is wrapped on a wheel of moment of inertia 0⋅20 kg-m2 and radius 10 cm and goes through a light pulley to support a block of mass 2⋅0 kg as shown in the following figure. Find the acceleration of the block.
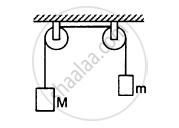
The pulleys shown in the following figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
A diver having a moment of inertia of 6⋅0 kg-m2 about an axis thorough its centre of mass rotates at an angular speed of 2 rad/s about this axis. If he folds his hands and feet to decrease the moment of inertia to 5⋅0 kg-m2, what will be the new angular speed?
A wheel of mass 15 kg has a moment of inertia of 200 kg-m2 about its own axis, the radius of gyration will be:
From a circular ring of mass, ‘M’ and radius ‘R’ an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR2’. Then the value of ‘K’ is ______.
Consider a badminton racket with length scales as shown in the figure.
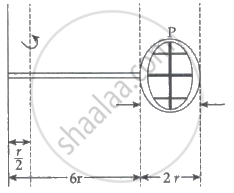
If the mass of the linear and circular portions of the badminton racket is the same (M) and the mass of the threads is negligible, the moment of inertia of the racket about an axis perpendicular to the handle and in the plane of the ring at, `r/2` distance from the ends A of the handle will be ______ Mr2.
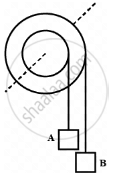
The figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then ______.