Advertisements
Advertisements
प्रश्न
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to be done to stop it?
उत्तर १
Radius of the hoop, r = 2 m
Mass of the hoop, m = 100 kg
Velocity of the hoop, v = 20 cm/s = 0.2 m/s
Total energy of the hoop = Translational KE + Rotational KE
`E_r = 1/2mv^2 + 1/2 Iomega^2`
Moment of inertia of the hoop about its centre, I = mr2
`E_r = 1/2 mv^2 + 1/2(mr^2)omega^2`
But we have the relation, `v = romega`
`:.E_r = 1/2 mv^2 + 1/2 mr^2omega^2`
`=1/2mv^2 + 1/2 mv^2 = mv^2`
The work required to be done for stopping the hoop is equal to the total energy of the hoop.
∴Required work to be done, W = mv2 = 100 × (0.2)2 = 4 J
उत्तर २
Here, R = 2 m, M = 100 kg
v = 20 cm/s = 0.2 m/s
Total energy of the hoop =1/2Mv2 + 1/2Iw2
=1/2Mv2 + 1/2(MR2)w2
=1/2Mv2 +1/2Mv2 =Mv2
Work required to stop the hoop = total energy of the hoop W = Mv2 = 100 (0.2)2= 4 Joule
APPEARS IN
संबंधित प्रश्न
Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
The oxygen molecule has a mass of 5.30 × 10–26 kg and a moment of inertia of 1.94×10–46 kg m2 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ω1 and ω2 are brought into contact face to face with their axes of rotation coincident. (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take ω1 ≠ ω2.
A string is wrapped on a wheel of moment of inertia 0⋅20 kg-m2 and radius 10 cm and goes through a light pulley to support a block of mass 2⋅0 kg as shown in the following figure. Find the acceleration of the block.
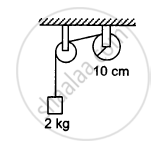
Suppose the smaller pulley of the previous problem has its radius 5⋅0 cm and moment of inertia 0⋅10 kg-m2. Find the tension in the part of the string joining the pulleys.
The descending pulley shown in the following figure has a radius 20 cm and moment of inertia 0⋅20 kg-m2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1⋅0 kg.
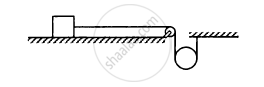
Solve the previous problem if the friction coefficient between the 2⋅0 kg block and the plane below it is 0⋅5 and the plane below the 4⋅0 kg block is frictionless.
From a circular ring of mass ‘M’ and radius ‘R’ an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR2’. Then the value of ‘K’ is ______.
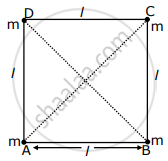
Four equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be ______.