Advertisements
Advertisements
प्रश्न
The oxygen molecule has a mass of 5.30 × 10–26 kg and a moment of inertia of 1.94×10–46 kg m2 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
उत्तर १
Mass of an oxygen molecule, m = 5.30 × 10–26 kg
Moment of inertia, I = 1.94 × 10–46 kg m2
Velocity of the oxygen molecule, v = 500 m/s
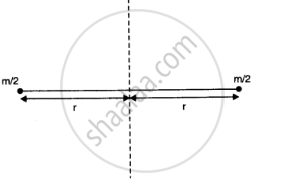
The separation between the two atoms of the oxygen molecule = 2r
Mass of each oxygen atom = `m/2`
Hence, moment of inertia I, is calculated as:
`(m/2)r^2 + (m/2)r^2 = mr^2`
r = `sqrt(I/m)`
`sqrt((1.94 xx 10^(-46))/(5.36 xx 10^(-26))) = 0.60 xx 10^(-10)m`
It is given that:
`KE_"rot" = KE_"trans`"`
`1/2 Iomega^2 =2/3 xx 1/2 "mv"^2`
`mr^2 omega^2 = 2/3 mv^2`
`omega = sqrt(2/3) v/r`
`= sqrt(2/3) xx 500/(0.6 xx 10^(-10))`
`= 6.80 xx 10^12 "rad/s"`
उत्तर २
`m = 5.30 xx 10^(-26)`
`I = 1.94 xx 10^(-46) kg m^2`
`v = 500 "m/s"`
if m/2 si mass of each of oxygen and 2r is distnace between the two atoms as shown in figure then.
`I = m/2 r^2 + m/2r^2 = mr^2`
`r = sqrt(I/m) = sqrt((1.94 xx 10^(-46))/(5.30 xx 10^(-26)))`
`= 0.61 xx 10^(-10) m`
As K.E of rotation = 2/3 K.E of transalation
`:. 1/2 Iomega^2 = 2/3 xx 1/2 momega^2`
`1/2(mr^2)omega^2 = 1/2 mv^2`
`omega = sqrt(2/3) v/r = sqrt(2/3) xx500 /(0.61xx10^(-10)) = 6.7 xx 10^(12) "rad/s"`
APPEARS IN
संबंधित प्रश्न
Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge
Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to be done to stop it?
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not.
A uniform metre stick of mass 200 g is suspended from the ceiling thorough two vertical strings of equal lengths fixed at the ends. A small object of mass 20 g is placed on the stick at a distance of 70 cm from the left end. Find the tensions in the two strings.
A diver having a moment of inertia of 6⋅0 kg-m2 about an axis thorough its centre of mass rotates at an angular speed of 2 rad/s about this axis. If he folds his hands and feet to decrease the moment of inertia to 5⋅0 kg-m2, what will be the new angular speed?
Two blocks of masses 400 g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has a moment of inertia \[1 \cdot 6 \times {10}^{- 4} kg - m^2\] and a radius 2⋅0 cm, Find (a) the kinetic energy of the system as the 400 g block falls through 50 cm, (b) the speed of the blocks at this instant.
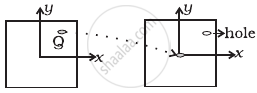
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind (Figure). The moment of inertia about the z-axis is then ______.
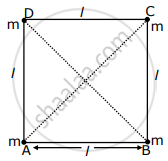
Four equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be ______.