Advertisements
Advertisements
प्रश्न
A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5 m/s.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
उत्तर १
Here, θ= 30°, v = 5 m/ s
Let the cylinder go up the plane up to a height h.
From 1/2 mv2 +1/2IW2 = mgh
`1/2 mv^2 + 1/2(1/2mr^2)omega^2 = mgh`
`3/4mv^2 = mgh`
`h = (3v^2)/(4g) = (3xx5^2)/(4xx9.8) = 1.913 m`
if s is the distance up the inclined plane, then as
`sin theta = h/s, s = h/(sin theta) = 1.913/sin 30^@ 3.856 m`
Time taken to return to the bottom
`t = sqrt((2s(1+k^2/r^2))/(g sin theta)) = sqrt((2xx 3826(1+1/2))/(9.8 sin 30^@)) = 1.53s`
उत्तर २
A solid cylinder rolling up an inclination is shown in the following figure.
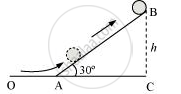
Initial velocity of the solid cylinder, v = 5 m/s
Angle of inclination, θ = 30°
Height reached by the cylinder = h
(a) Energy of the cylinder at point A:
`KE_"rot" = KE_"trans"`
`1/2 Iomega^2 = 1/2 mv^2`
Energy of the cylinder at point B = mgh
Using the law of conservation of energy, we can write:
`1/2Iomega^2 = 1/2mv^2 = mgh`
Moment of inertia of the solid cylinder, `I = 1/2 mr^2`
`:.1/2(1/2 mr^2)omega^2 + 1/2 mv^2 = mgh`
`1/4 mr^2 omega^2 + 1/2 mv^2 = mgh`
But we have the relation `v = romega`
`:.1/4v^2 + 1/2v^2 = gh`
`3/4 v^2 =gh`
`:.h = 3/4 v^2/g`
`= 3/4 xx (5xx5)/(9.8) = 1.91 m`
In `triangleABC`
`sin theta = (BC)/(AB)`
`sin 30^@ = h/(AB)`
`AB = (1.91)/0.5 = 3.82 m`
Hence, the cylinder will travel 3.82 m up the inclined plane.
(b) For radius of gyration K, the velocity of the cylinder at the instance when it rolls back to the bottom is given by the relation:
`v = ((2gh)/(1+K^2/R^2))^(1/2)`
`:.v = ((2gABsin theta)/(1+K^2/R^2))^(1/2)`
For the soild cylinder, `K^2 = R^2/2`
`:.v = ((2gABsin theta)/(1+1/2))^(1/2)`
`= (4/3gABsin theta)^(1/2)`
The time taken to return to the bottom is:
`t = (AB)/v`
`= (AB)/(4/3gABsintheta)^(1/2) =((3AB)/(4gsintheta))^"1/2"`
`=(11.46/19.6)^(1/2) = 0.764 s`
Therefore, the total time taken by the cylinder to return to the bottom is (2 × 0.764) 1.53 s.
APPEARS IN
संबंधित प्रश्न
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value? Assume that the turntable rotates without friction.
Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
The oxygen molecule has a mass of 5.30 × 10–26 kg and a moment of inertia of 1.94×10–46 kg m2 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
A string is wrapped on a wheel of moment of inertia 0⋅20 kg-m2 and radius 10 cm and goes through a light pulley to support a block of mass 2⋅0 kg as shown in the following figure. Find the acceleration of the block.
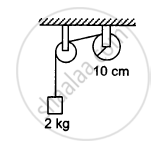
A uniform metre stick of mass 200 g is suspended from the ceiling thorough two vertical strings of equal lengths fixed at the ends. A small object of mass 20 g is placed on the stick at a distance of 70 cm from the left end. Find the tensions in the two strings.
A boy is seated in a revolving chair revolving at an angular speed of 120 revolutions per minute. Two heavy balls form part of the revolving system and the boy can pull the balls closer to himself or may push them apart. If by pulling the balls closer, the boy decreases the moment of inertia of the system from 6 kg-m2 to 2 kg-m2, what will be the new angular speed?
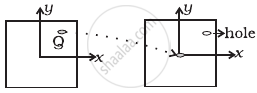
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind (Figure). The moment of inertia about the z-axis is then ______.
A thin circular plate of mass M and radius R has its density varying as ρ(r) = ρ0r with ρ0 as constant and r is the distance from its center. The moment of Inertia of the circular plate about an axis perpendicular to the plate and passing through its edge is I = a MR2. The value of the coefficient a is ______.
A cubical block of mass 6 kg and side 16.1 cm is placed on a frictionless horizontal surface. It is hit by a cue at the top to impart impulse in the horizontal direction. The minimum impulse imparted to topple the block must be greater than ______ kg m/s.
