Advertisements
Advertisements
Question
A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5 m/s.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
Advertisements
Solution 1
Here, θ= 30°, v = 5 m/ s
Let the cylinder go up the plane up to a height h.
From 1/2 mv2 +1/2IW2 = mgh
`1/2 mv^2 + 1/2(1/2mr^2)omega^2 = mgh`
`3/4mv^2 = mgh`
`h = (3v^2)/(4g) = (3xx5^2)/(4xx9.8) = 1.913 m`
if s is the distance up the inclined plane, then as
`sin theta = h/s, s = h/(sin theta) = 1.913/sin 30^@ 3.856 m`
Time taken to return to the bottom
`t = sqrt((2s(1+k^2/r^2))/(g sin theta)) = sqrt((2xx 3826(1+1/2))/(9.8 sin 30^@)) = 1.53s`
Solution 2
A solid cylinder rolling up an inclination is shown in the following figure.
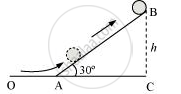
Initial velocity of the solid cylinder, v = 5 m/s
Angle of inclination, θ = 30°
Height reached by the cylinder = h
(a) Energy of the cylinder at point A:
`KE_"rot" = KE_"trans"`
`1/2 Iomega^2 = 1/2 mv^2`
Energy of the cylinder at point B = mgh
Using the law of conservation of energy, we can write:
`1/2Iomega^2 = 1/2mv^2 = mgh`
Moment of inertia of the solid cylinder, `I = 1/2 mr^2`
`:.1/2(1/2 mr^2)omega^2 + 1/2 mv^2 = mgh`
`1/4 mr^2 omega^2 + 1/2 mv^2 = mgh`
But we have the relation `v = romega`
`:.1/4v^2 + 1/2v^2 = gh`
`3/4 v^2 =gh`
`:.h = 3/4 v^2/g`
`= 3/4 xx (5xx5)/(9.8) = 1.91 m`
In `triangleABC`
`sin theta = (BC)/(AB)`
`sin 30^@ = h/(AB)`
`AB = (1.91)/0.5 = 3.82 m`
Hence, the cylinder will travel 3.82 m up the inclined plane.
(b) For radius of gyration K, the velocity of the cylinder at the instance when it rolls back to the bottom is given by the relation:
`v = ((2gh)/(1+K^2/R^2))^(1/2)`
`:.v = ((2gABsin theta)/(1+K^2/R^2))^(1/2)`
For the soild cylinder, `K^2 = R^2/2`
`:.v = ((2gABsin theta)/(1+1/2))^(1/2)`
`= (4/3gABsin theta)^(1/2)`
The time taken to return to the bottom is:
`t = (AB)/v`
`= (AB)/(4/3gABsintheta)^(1/2) =((3AB)/(4gsintheta))^"1/2"`
`=(11.46/19.6)^(1/2) = 0.764 s`
Therefore, the total time taken by the cylinder to return to the bottom is (2 × 0.764) 1.53 s.
RELATED QUESTIONS
Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value? Assume that the turntable rotates without friction.
Let I1 an I2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminium and the second of iron.
Suppose the smaller pulley of the previous problem has its radius 5⋅0 cm and moment of inertia 0⋅10 kg-m2. Find the tension in the part of the string joining the pulleys.
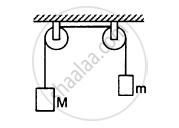
The pulley shown in the following figure has a radius 10 cm and moment of inertia 0⋅5 kg-m2about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4⋅0 kg block.
A boy is seated in a revolving chair revolving at an angular speed of 120 revolutions per minute. Two heavy balls form part of the revolving system and the boy can pull the balls closer to himself or may push them apart. If by pulling the balls closer, the boy decreases the moment of inertia of the system from 6 kg-m2 to 2 kg-m2, what will be the new angular speed?
A wheel of moment of inertia 0⋅10 kg-m2 is rotating about a shaft at an angular speed of 160 rev/minute. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with a common angular speed of 200 rev/minute. Find the moment of inertia of the second wheel.
Two blocks of masses 400 g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has a moment of inertia \[1 \cdot 6 \times {10}^{- 4} kg - m^2\] and a radius 2⋅0 cm, Find (a) the kinetic energy of the system as the 400 g block falls through 50 cm, (b) the speed of the blocks at this instant.
The pulley shown in the following figure has a radius of 20 cm and moment of inertia 0⋅2 kg-m2. The string going over it is attached at one end to a vertical spring of spring constant 50 N/m fixed from below, and supports a 1 kg mass at the other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has descended through 10 cm. Take g = 10 m/s2.
A wheel of mass 15 kg has a moment of inertia of 200 kg-m2 about its own axis, the radius of gyration will be:
From a circular ring of mass ‘M’ and radius ‘R’ an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR2’. Then the value of ‘K’ is ______.
Why does a solid sphere have smaller moment of inertia than a hollow cylinder of same mass and radius, about an axis passing through their axes of symmetry?
Moment of inertia (M.I.) of four bodies, having same mass and radius, are reported as :
I1 = M.I. of thin circular ring about its diameter,
I2 = M.I. of circular disc about an axis perpendicular to disc and going through the centre,
I3 = M.I. of solid cylinder about its axis and
I4 = M.I. of solid sphere about its diameter.
Then -
Consider a badminton racket with length scales as shown in the figure.
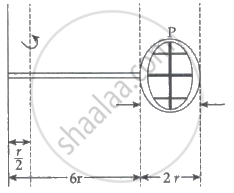
If the mass of the linear and circular portions of the badminton racket is the same (M) and the mass of the threads is negligible, the moment of inertia of the racket about an axis perpendicular to the handle and in the plane of the ring at, `r/2` distance from the ends A of the handle will be ______ Mr2.
A thin circular plate of mass M and radius R has its density varying as ρ(r) = ρ0r with ρ0 as constant and r is the distance from its center. The moment of Inertia of the circular plate about an axis perpendicular to the plate and passing through its edge is I = a MR2. The value of the coefficient a is ______.
A cubical block of mass 6 kg and side 16.1 cm is placed on a frictionless horizontal surface. It is hit by a cue at the top to impart impulse in the horizontal direction. The minimum impulse imparted to topple the block must be greater than ______ kg m/s.
