Advertisements
Advertisements
Question
A boy is seated in a revolving chair revolving at an angular speed of 120 revolutions per minute. Two heavy balls form part of the revolving system and the boy can pull the balls closer to himself or may push them apart. If by pulling the balls closer, the boy decreases the moment of inertia of the system from 6 kg-m2 to 2 kg-m2, what will be the new angular speed?
Solution
Given
Initial angular speed of the system,
\[\omega_1 = 120\text{ rpm }= 120 \times \left( \frac{2\pi}{60} \right) = 4\pi\text{ rad/s}\]
Initial moment of inertia of the system,
\[I_1 = 6 kg - m^2\]
Final moment of inertia of the system,
\[I_2 = 2 kg - m^2\]
Two balls are inside the system; therefore, we get
Total external torque = 0
\[I_2 = 2 kg - m^2\]
\[\therefore I_1 \omega_1 = I_2 \omega_2\]
\[\Rightarrow 6 \times 4\pi = 2 \omega_2 \]
\[ \Rightarrow \omega_2 = 12\pi rad/s\]
\[\text{Or, }\omega_2 = 6\text{ rev/s }= 360\text{ rev/minute}\]
APPEARS IN
RELATED QUESTIONS
Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ω1 and ω2 are brought into contact face to face with their axes of rotation coincident. (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take ω1 ≠ ω2.
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction µs = 0.25.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is ___________ .
Let I1 an I2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminium and the second of iron.
A body having its centre of mass at the origin has three of its particles at (a,0,0), (0,a,0), (0,0,a). The moments of inertia of the body about the X and Y axes are 0⋅20 kg-m2 each. The moment of inertia about the Z-axis
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not.
A string is wrapped on a wheel of moment of inertia 0⋅20 kg-m2 and radius 10 cm and goes through a light pulley to support a block of mass 2⋅0 kg as shown in the following figure. Find the acceleration of the block.
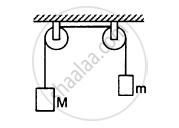
The pulleys shown in the following figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
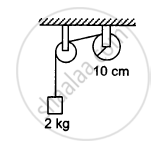
The descending pulley shown in the following figure has a radius 20 cm and moment of inertia 0⋅20 kg-m2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1⋅0 kg.
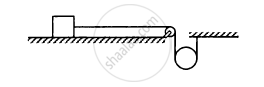
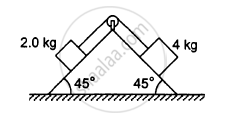
The pulley shown in the following figure has a radius 10 cm and moment of inertia 0⋅5 kg-m2about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4⋅0 kg block.
A diver having a moment of inertia of 6⋅0 kg-m2 about an axis thorough its centre of mass rotates at an angular speed of 2 rad/s about this axis. If he folds his hands and feet to decrease the moment of inertia to 5⋅0 kg-m2, what will be the new angular speed?
A kid of mass M stands at the edge of a platform of radius R which can be freely rotated about its axis. The moment of inertia of the platform is I. The system is at rest when a friend throws a ball of mass m and the kid catches it. If the velocity of the ball is \[\nu\] horizontally along the tangent to the edge of the platform when it was caught by the kid, find the angular speed of the platform after the event.
Two blocks of masses 400 g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has a moment of inertia \[1 \cdot 6 \times {10}^{- 4} kg - m^2\] and a radius 2⋅0 cm, Find (a) the kinetic energy of the system as the 400 g block falls through 50 cm, (b) the speed of the blocks at this instant.
Four bodies of masses 2 kg, 3 kg, 4 kg and 5 kg are placed at points A, B, C, and D respectively of a square ABCD of side 1 metre. The radius of gyration of the system about an axis passing through A and perpendicular to plane is
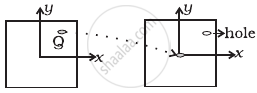
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind (Figure). The moment of inertia about the z-axis is then ______.
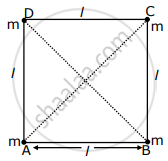
Four equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be ______.
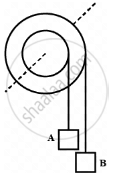
The figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then ______.