Advertisements
Advertisements
Question
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction µs = 0.25.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
Solution
Mass of the cylinder, m = 10 kg
Radius of the cylinder, r = 15 cm = 0.15 m
Co-efficient of kinetic friction, µk = 0.25
Angle of inclination, θ = 30°
Moment of inertia of a solid cylinder about its geometric axis, I = 1/2 mr2
The various forces acting on the cylinder are shown in the following figure:
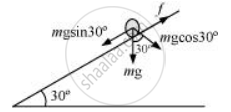
The acceleration of the cylinder is given as:
`a = (mg sin theta)/(m + I/r^2)`
= `(mg sin theta)/(m+1/2 mr^2/r^2) = 2/3 g sin 30^@`
`= 2/3 xx 9.8 xx 05 = 3.27 "m/s"^2`
a) Using Newton’s second law of motion, we can write net force as:
fnet = ma
`mg sin 30^@ - f = ma`
`f =mg sin30^@ - ma`
= 10 x 9.8 x 0.5- 10 x 3.27
= 49 -32.7 = 16.3 N
b) During rolling, the instantaneous point of contact with the plane comes to rest. Hence, the work done against frictional force is zero.
c) For rolling without skid, we have the relation:
`mu = 1/3 tan theta`
`tan theta = 3 mu = 3 xx 0.25`
`: theta = tan^(-1) (0.75) = 36.87^@`
APPEARS IN
RELATED QUESTIONS
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to be done to stop it?
Suppose the smaller pulley of the previous problem has its radius 5⋅0 cm and moment of inertia 0⋅10 kg-m2. Find the tension in the part of the string joining the pulleys.
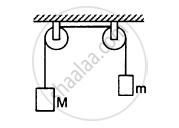
The pulleys shown in the following figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
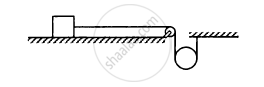
The descending pulley shown in the following figure has a radius 20 cm and moment of inertia 0⋅20 kg-m2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1⋅0 kg.
From a circular ring of mass ‘M’ and radius ‘R’ an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR2 ’. Then the value of ‘K’ is ______.
With reference to figure of a cube of edge a and mass m, state whether the following are true or false. (O is the centre of the cube.)
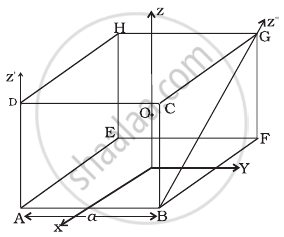
- The moment of inertia of cube about z-axis is Iz = Ix + Iy
- The moment of inertia of cube about z ′ is I'z = `I_z + (ma^2)/2`
- The moment of inertia of cube about z″ is = `I_z + (ma^2)/2`
- Ix = Iy
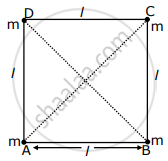
Four equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be ______.
Consider a badminton racket with length scales as shown in the figure.
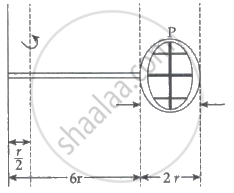
If the mass of the linear and circular portions of the badminton racket is the same (M) and the mass of the threads is negligible, the moment of inertia of the racket about an axis perpendicular to the handle and in the plane of the ring at, `r/2` distance from the ends A of the handle will be ______ Mr2.
