Advertisements
Advertisements
Question
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
Solution 1
Let M be the mass and R the radius of the hollow cylinder, and also of the solid sphere. Their moments of inertia about the respective axes are I1 = MR2 and I2 = 2/5 MR2
Let τ be the magnitude of the torque applied to the cylinder and the sphere, producing angular accelerations α1and α2 respectively. Then τ=I1 α1 = I2 α2
The angular acceleration 04 produced in the sphere is larger. Hence, the sphere will acquire larger angular speed after a given time.
Solution 2
Let m and r be the respective masses of the hollow cylinder and the solid sphere.
The moment of inertia of the hollow cylinder about its standard axis, `I_1 = mr^2`
The moment of inertia of the solid sphere about an axis passing through its centre,` I_n = 2/5 mr^2`
We have the relation:
`t = Ialpha`
Where
`alpha` = Angular acceleration
τ = Torque
I = Moment of inertia
For the hollow cylinder, `t_1 = I_1alpha1`
For the solid sphere, `t_n = I_nalpha_n`
As an equal torque is applied to both the bodies,` t_1 = t_2`
`:.(alpha_II)/(alpha_I) = (I_I)/(I_"II") = (mr^2)/(2/5mr^2) =2/5`
`alpha_(II) > alpha_I` ...(i)
Now, using the relation:
`omega = omega_0 + alpha t`
where
`omega_0` = Initial angular velocity
t = Time of rotation
ω = Final angular velocity
For equal ω0 and t, we have:
ω ∝ α … (ii)
From equations (i) and (ii), we can write:
ωII > ωI
Hence, the angular velocity of the solid sphere will be greater than that of the hollow cylinder
APPEARS IN
RELATED QUESTIONS
Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
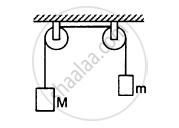
The pulleys shown in the following figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
A diver having a moment of inertia of 6⋅0 kg-m2 about an axis thorough its centre of mass rotates at an angular speed of 2 rad/s about this axis. If he folds his hands and feet to decrease the moment of inertia to 5⋅0 kg-m2, what will be the new angular speed?
A boy is seated in a revolving chair revolving at an angular speed of 120 revolutions per minute. Two heavy balls form part of the revolving system and the boy can pull the balls closer to himself or may push them apart. If by pulling the balls closer, the boy decreases the moment of inertia of the system from 6 kg-m2 to 2 kg-m2, what will be the new angular speed?
Four bodies of masses 2 kg, 3 kg, 4 kg and 5 kg are placed at points A, B, C, and D respectively of a square ABCD of side 1 metre. The radius of gyration of the system about an axis passing through A and perpendicular to plane is
From a circular ring of mass ‘M’ and radius ‘R’ an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR2’. Then the value of ‘K’ is ______.
Why does a solid sphere have smaller moment of inertia than a hollow cylinder of same mass and radius, about an axis passing through their axes of symmetry?
Moment of inertia (M.I.) of four bodies, having same mass and radius, are reported as :
I1 = M.I. of thin circular ring about its diameter,
I2 = M.I. of circular disc about an axis perpendicular to disc and going through the centre,
I3 = M.I. of solid cylinder about its axis and
I4 = M.I. of solid sphere about its diameter.
Then -
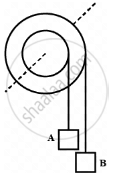
The figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then ______.