Advertisements
Advertisements
Question
A solid cylinder of mass 20 kg rotates about its axis with angular speed 100 rad s–1. The radius of the cylinder is 0.25 m. What is the kinetic energy associated with the rotation of the cylinder? What is the magnitude of the angular momentum of the cylinder about its axis?
Solution 1
Mass of the cylinder, m = 20 kg
Angular speed, ω = 100 rad s–1
Radius of the cylinder, r = 0.25 m
The moment of inertia of the solid cylinder:
`I = (mr^2)/2`
`= 1/2 xx 20 xx (0.25)^2`
= 0.625 `"kg m"^2`
:.Kinetic energy = `1/2Iomega^2`
`= 1/2 xx 6.25 xx (100)^2 = 3125J`
∴Angular momentum, L = Iω
= 6.25 × 100
= 62.5 Js
Solution 2
M = 20 kg
Angular speed, w = 100 rad s-1; R = 0.25 m
Moment of inertia of the cylinder about its axis =1/2 MR2 = 1/2 x 20 (0.25)2 kg m2 = 0.625 kg m2
Rotational kinetic energy,
Er = 1/2 Iw2 = 1/2 x 0.625 x (100)2 J = 3125 J
Angular momentum, L = Iw = 0.625 x 100 Js= 62.5 Js
APPEARS IN
RELATED QUESTIONS
Find the components along the x, y, z axes of the angular momentum l of a particle, whose position vector is r with components x, y, z and momentum is p with components px, py and 'p_z`. Show that if the particle moves only in the x-y plane the angular momentum has only a z-component.
Two particles, each of mass m and speed v, travel in opposite directions along parallel lines separated by a distance d. Show that the angular momentum vector of the two particle system is the same whatever be the point about which the angular momentum is taken.
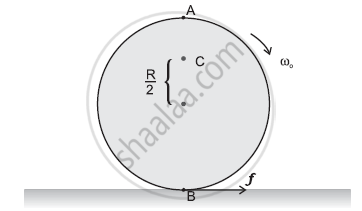
Explain why friction is necessary to make the disc in Figure roll in the direction indicated
(a) Give the direction of frictional force at B, and the sense of frictional torque, before perfect rolling begins.
(b) What is the force of friction after perfect rolling begins?
The torque of the weight of any body about any vertical axis is zero. If it always correct?
The torque of a force \[\overrightarrow F \] about a point is defined as \[\overrightarrow\Gamma = \overrightarrow r \times \overrightarrow F.\] Suppose \[\overrightarrow r, \overrightarrow F\] and \[\overrightarrow \Gamma\] are all nonzero. Is \[r \times \overrightarrow\Gamma || \overrightarrow F\] always true? Is it ever true?
A rectangular brick is kept on a table with a part of its length projecting out. It remains at rest if the length projected is slightly less than half the total length but it falls down if the length projected is slightly more than half the total length. Give reason.
The density of a rod gradually decreases from one end to the other. It is pivoted at an end so that it can move about a vertical axis though the pivot. A horizontal force F is applied on the free end in a direction perpendicular to the rod. The quantities, that do not depend on which end of the rod is pivoted, are ________________ .
Two discs of the same moment of inertia rotating about their regular axis passing through centre and perpendicular to the plane of the disc with angular velocities ω1 and ω2. They are brought in to contact face to face coinciding with the axis of rotation. The expression for loss of energy during this process is, ______
Choose the correct alternatives:
- For a general rotational motion, angular momentum L and angular velocity ω need not be parallel.
- For a rotational motion about a fixed axis, angular momentum L and angular velocity ω are always parallel.
- For a general translational motion , momentum p and velocity v are always parallel.
- For a general translational motion, acceleration a and velocity v are always parallel.
A uniform cube of mass m and side a is placed on a frictionless horizontal surface. A vertical force F is applied to the edge as shown in figure. Match the following (most appropriate choice):
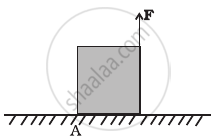
| (a) mg/4 < F < mg/2 | (i) Cube will move up. |
| (b) F > mg/2 | (ii) Cube will not exhibit motion. |
| (c) F > mg | (iii) Cube will begin to rotate and slip at A. |
| (d) F = mg/4 | (iv) Normal reaction effectively at a/3 from A, no motion. |
