Advertisements
Advertisements
Question
Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
Solution
`"Final Kinetic Energy of rotation"/"Initial Kinetic Energy of rotation" = (1/2 I_2omega_2^2)/(1/2I_1omega_1^2) = (1/2 I_2(2piv_2)^2)/(1/2I_1(2piv_1)^2) = (I_2v_2^2)/(I_1v_1^2) = (2/5I_1xx(100)^2)/(2/5I_1xx(40)^2) = 2.5`
Clearly, final (K.E) becomes more because the child used his internal energy when he folds his hands to increase the kinetic energy
APPEARS IN
RELATED QUESTIONS
Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ω1 and ω2 are brought into contact face to face with their axes of rotation coincident. (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take ω1 ≠ ω2.
A body having its centre of mass at the origin has three of its particles at (a,0,0), (0,a,0), (0,0,a). The moments of inertia of the body about the X and Y axes are 0⋅20 kg-m2 each. The moment of inertia about the Z-axis
Suppose the smaller pulley of the previous problem has its radius 5⋅0 cm and moment of inertia 0⋅10 kg-m2. Find the tension in the part of the string joining the pulleys.
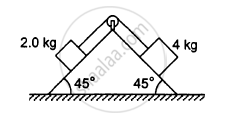
The pulley shown in the following figure has a radius 10 cm and moment of inertia 0⋅5 kg-m2about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4⋅0 kg block.
A wheel of moment of inertia 0⋅500 kg-m2 and radius 20⋅0 cm is rotating about its axis at an angular speed of 20⋅0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
A wheel of moment of inertia 0⋅10 kg-m2 is rotating about a shaft at an angular speed of 160 rev/minute. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with a common angular speed of 200 rev/minute. Find the moment of inertia of the second wheel.
A wheel of mass 15 kg has a moment of inertia of 200 kg-m2 about its own axis, the radius of gyration will be:
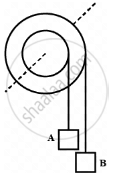
The figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then ______.