Advertisements
Advertisements
Question
Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge
Solution 1
The moment of inertia of disc about its diameter =
According to the theorem of the perpendicular axis, the moment of inertia of a planar body (lamina) about an axis perpendicular to its plane is equal to the sum of its moments of inertia about two perpendicular axes concurrent with the perpendicular axis and lying in the plane of the body.
The M.I of the disc about its centre =
The situation is shown in the given figure
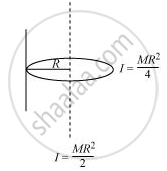
Applying the theorem of parallel axes:
The moment of inertia about an axis normal to the disc and passing through a point on its edge
Solution 2
We are given, moment of inertia of the disc about any of its diameters = 1/4 MR2
(i) Using theorem of perpendicular axes, moment of inertia of the disc about an axis passing through its centre and normal to the disc = 2 x 1/4 MR2 = 1/2 MR2
(ii) Using theorem axes, moment of inertia of the disc passing through a point on its edge and normal to the dies = 1/2 MR2+ MR2 = 3/2 MR2.
APPEARS IN
RELATED QUESTIONS
Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
The oxygen molecule has a mass of 5.30 × 10–26 kg and a moment of inertia of 1.94×10–46 kg m2 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.
(Hint: The moment of inertia of the door about the vertical axis at one end is ML2/3.)
The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is ___________ .
Suppose the smaller pulley of the previous problem has its radius 5⋅0 cm and moment of inertia 0⋅10 kg-m2. Find the tension in the part of the string joining the pulleys.
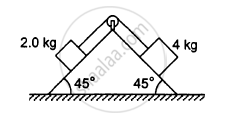
The pulley shown in the following figure has a radius 10 cm and moment of inertia 0⋅5 kg-m2about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4⋅0 kg block.
A kid of mass M stands at the edge of a platform of radius R which can be freely rotated about its axis. The moment of inertia of the platform is I. The system is at rest when a friend throws a ball of mass m and the kid catches it. If the velocity of the ball is
Two blocks of masses 400 g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has a moment of inertia
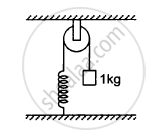
The pulley shown in the following figure has a radius of 20 cm and moment of inertia 0⋅2 kg-m2. The string going over it is attached at one end to a vertical spring of spring constant 50 N/m fixed from below, and supports a 1 kg mass at the other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has descended through 10 cm. Take g = 10 m/s2.
Consider a badminton racket with length scales as shown in the figure.
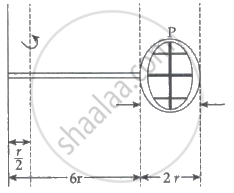
If the mass of the linear and circular portions of the badminton racket is the same (M) and the mass of the threads is negligible, the moment of inertia of the racket about an axis perpendicular to the handle and in the plane of the ring at,
