Advertisements
Advertisements
Question
As shown in Fig.7.40, the two sides of a step ladder BA and CA are 1.6 m long and hinged at A. A rope DE, 0.5 m is tied half way up. A weight 40 kg is suspended from a point F, 1.2 m from B along the ladder BA. Assuming the floor to be frictionless and neglecting the weight of the ladder, find the tension in the rope and forces exerted by the floor on the ladder. (Take g = 9.8 m/s2)
(Hint: Consider the equilibrium of each side of the ladder separately.)
Solution 1
The given situation can be shown as:
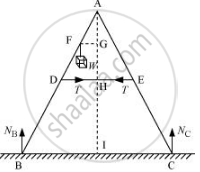
NB = Force exerted on the ladder by the floor point B
NC = Force exerted on the ladder by the floor point C
T = Tension in the rope
BA = CA = 1.6 m
DE = 0. 5 m
BF = 1.2 m
Mass of the weight, m = 40 kg
Draw a perpendicular from A on the floor BC. This intersects DE at mid-point H.
ΔABI and ΔAIC are similar
∴BI = IC
Hence, I is the mid-point of BC.
DE || BC
BC = 2 × DE = 1 m
AF = BA – BF = 0.4 m … (i)
D is the mid-point of AB.
Hence, we can write:
`AD = 1/2xxBA = 0.8 m` we get ..(ii)
Using equations (i) and (ii), we get:
FE = 0.4 m
Hence, F is the mid-point of AD.
FG||DH and F is the mid-point of the AD. Hence, G will also be the mid-point of AH.
ΔAFG and ΔADH are similar
`:.(FG)/(DH) =(AF)/(AD)`
`(FG)/(DH) = 0.4/0.8 = 1/2`
`FG = 1/2 DH`
`=- 1.2 xx 0.25 = 0.125 m`
In ΔADH:
`AH = sqrt((AD)^2 - (DH)^2)`
`= sqrt((0.8)^2 - (0.25)^2) = 0.76 m`
For translational equilibrium of the ladder, the upward force should be equal to the downward force.
Nc + NB = mg = 392 … (iii)
For rotational equilibrium of the ladder, the net moment about A is:
`-N_BxxBI+mg xxFG+N_c xx CI + T xx AG - T xx AG = 0`
`-N_Bxx 0.5 + 40 xx 9.8 xx 0.125 + N_c xx (0.5) = 0`
(N_c- N_a) = 98 .. (iv)
Adding equations (iii) and (iv), we get:
`N_c = 245 N`
`N_n = 147 N`
For rotational equilibrium of the side AB, consider the moment about A
`-N_B xx BI + mg xx FG + T xx AG = 0`
`-245 xx 05 + 40 + 9.8 xx 0.125 + T xx 0.76 = 0`
0.76T = 122.5 - 49
`:.T = 96.7 N`
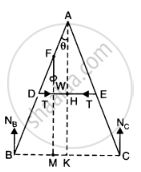
Solution 2
The forces acting on the ladder are shown in Fig. 7.14.Here, IV = 40 kg = 40 x 9.8 N = 392 N, AB = AC = 1.6 m, BD = 1/2 x 1.6 m = 0.8 m,
BF = 1.2 m and DE 0.5 m,
In figure `triangleADE` and `triangleABC` are similar hence
`BC = DE xx (AB)/(AD) = (0.5 xx 1.6)/0.8 = 1.0 m`
Now considering equilibrium at apoint B, `sumt = 0`
`:. W xx (MB) = N_c xx (CB)` ...... (i)
But `MB = (KB xx BF)/(BA) = (0.5 xx 1.2)/1.6 = 0.375 m`
Substituting this value in (i) we get
`:.N_C = (Wxx(MB))/(CB) = (392xx .0375)/1 = 147 N`
Again considering equilibrium at point C in similar manner we have
`W xx (MC) = N_B xx (BC)`
`:.N_B = (Wxx(MC))/(BC) = (Wxx(BC - BM))/(BC)`
=(392 x (1-0.375))/1=245 N
Now, it can be easily shown that tension in the string
T = NB – NC = 245 – 147 = 98 N
APPEARS IN
RELATED QUESTIONS
A car weighs 1800 kg. The distance between its front and back axles is 1.8 m. Its centre of gravity is 1.05 m behind the front axle. Determine the force exerted by the level ground on each front wheel and each back wheel.
From a uniform disk of radius R, a circular hole of radius R/2 is cut out. The centre of the hole is at R/2 from the centre of the original disc. Locate the centre of gravity of the resulting flat body.
A metre stick is balanced on a knife edge at its centre. When two coins, each of mass 5 g are put one on top of the other at the 12.0 cm mark, the stick is found to be balanced at 45.0 cm. What is the mass of the metre stick?
If the sum of all the forces acting on a body is zero, is it necessarily in equilibrium? If the sum of all the forces on a particle is zero, is it necessarily in equilibrium?
A uniform ladder of length 10⋅0 m and mass 16⋅0 kg is resting against a vertical wall making an angle of 37° with it. The vertical wall is frictionless but the ground is rough. An electrician weighing 60⋅0 kg climbs up the ladder. If he stays on the ladder at a point 8⋅00 m from the lower end, what will be the normal force and the force of friction on the ladder by the ground? What should be the minimum coefficient of friction for the electrician to work safely?
Suppose the friction coefficient between the ground and
the ladder of the previous problem is 0.540. Find the
maximum weight of a mechanic who could go up and do
the work from the same position of the ladder.
The door of an almirah is 6 ft high, 1⋅5 ft wide and weighs 8 kg. The door is supported by two hinges situated at a distance of 1 ft from the ends. If the magnitudes of the forces exerted by the hinges on the door are equal, find this magnitude.
A rod of weight W is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at a distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is
The centre of gravity of a body on the earth coincides with its centre of mass for a ‘small’ object whereas for an ‘extended’ object it may not. What is the qualitative meaning of ‘small’ and ‘extended’ in this regard? For which of the following the two coincides? A building, a pond, a lake, a mountain?
The vector sum of a system of non-collinear forces acting on a rigid body is given to be non-zero. If the vector sum of all the torques due to the system of forces about a certain point is found to be zero, does this mean that it is necessarily zero about any arbitrary point?
