Advertisements
Advertisements
प्रश्न
A diver having a moment of inertia of 6⋅0 kg-m2 about an axis thorough its centre of mass rotates at an angular speed of 2 rad/s about this axis. If he folds his hands and feet to decrease the moment of inertia to 5⋅0 kg-m2, what will be the new angular speed?
उत्तर
Initial moment of inertia of diver, I1 = 6 kg-m2
Initial angular velocity of diver, ω1 = 2 rad/s
Final moment of inertia of diver, I2 = 5 kg-m2
Let ω2 be the final angular velocity of the diver.
We have
External torque = 0
∴ I1ω1 = I2ω2
\[\Rightarrow \omega_2 = \frac{6 \times 2}{5} = 2.4 \text{ rad/s}\]
APPEARS IN
संबंधित प्रश्न
Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5 m/s.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ω1 and ω2 are brought into contact face to face with their axes of rotation coincident. (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take ω1 ≠ ω2.
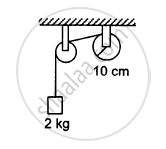
A string is wrapped on a wheel of moment of inertia 0⋅20 kg-m2 and radius 10 cm and goes through a light pulley to support a block of mass 2⋅0 kg as shown in the following figure. Find the acceleration of the block.
The pulley shown in the following figure has a radius 10 cm and moment of inertia 0⋅5 kg-m2about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4⋅0 kg block.
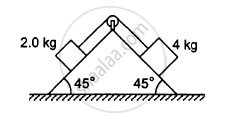
Solve the previous problem if the friction coefficient between the 2⋅0 kg block and the plane below it is 0⋅5 and the plane below the 4⋅0 kg block is frictionless.
A uniform metre stick of mass 200 g is suspended from the ceiling thorough two vertical strings of equal lengths fixed at the ends. A small object of mass 20 g is placed on the stick at a distance of 70 cm from the left end. Find the tensions in the two strings.
A wheel of moment of inertia 0⋅500 kg-m2 and radius 20⋅0 cm is rotating about its axis at an angular speed of 20⋅0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
A kid of mass M stands at the edge of a platform of radius R which can be freely rotated about its axis. The moment of inertia of the platform is I. The system is at rest when a friend throws a ball of mass m and the kid catches it. If the velocity of the ball is \[\nu\] horizontally along the tangent to the edge of the platform when it was caught by the kid, find the angular speed of the platform after the event.
From a circular ring of mass, ‘M’ and radius ‘R’ an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR2’. Then the value of ‘K’ is ______.
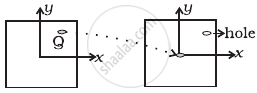
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind (Figure). The moment of inertia about the z-axis is then ______.
With reference to figure of a cube of edge a and mass m, state whether the following are true or false. (O is the centre of the cube.)
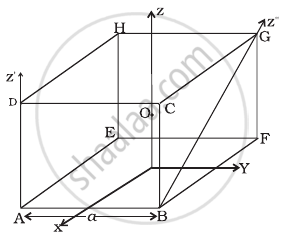
- The moment of inertia of cube about z-axis is Iz = Ix + Iy
- The moment of inertia of cube about z ′ is I'z = `I_z + (ma^2)/2`
- The moment of inertia of cube about z″ is = `I_z + (ma^2)/2`
- Ix = Iy
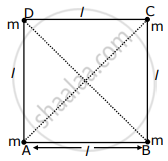
Four equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be ______.
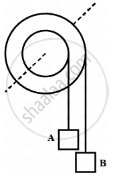
The figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then ______.