Advertisements
Advertisements
प्रश्न
Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
उत्तर १
`7/5 MR^2`
The moment of inertia (M.I.) of a sphere about its diameter = `2/5 MR^2`
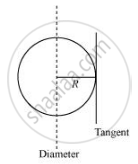
`ML = 2/5MR^2`
According to the theorem of parallel axes, the moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.
The M.I. about a tangent of the sphere = `2/5 MR^2 + MR^2 = 7/5 MR^2`
उत्तर २
Moment of inertia of sphere about any diameter = 2/5 MR2
Applying theorem of parallel axes, Moment of inertia of sphere about a tangent to the sphere = 2/5MR2 +M(R)2 =7/5 MR2
APPEARS IN
संबंधित प्रश्न
A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value? Assume that the turntable rotates without friction.
Show that the child’s new kinetic energy of rotation is more than the initial kinetic energy of rotation. How do you account for this increase in kinetic energy?
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction µs = 0.25.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
Let I1 an I2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminium and the second of iron.
The pulley shown in the following figure has a radius 10 cm and moment of inertia 0⋅5 kg-m2about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4⋅0 kg block.
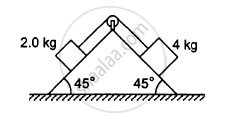
Solve the previous problem if the friction coefficient between the 2⋅0 kg block and the plane below it is 0⋅5 and the plane below the 4⋅0 kg block is frictionless.
A wheel of moment of inertia 0⋅10 kg-m2 is rotating about a shaft at an angular speed of 160 rev/minute. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with a common angular speed of 200 rev/minute. Find the moment of inertia of the second wheel.
A wheel of mass 15 kg has a moment of inertia of 200 kg-m2 about its own axis, the radius of gyration will be:
From a circular ring of mass ‘M’ and radius ‘R’ an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR2’. Then the value of ‘K’ is ______.
