Advertisements
Advertisements
प्रश्न
Let I1 an I2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminium and the second of iron.
पर्याय
I1 < I2
I1 = I2
I1 > I2
relation between I1 and I2 depends on the actual shapes of the bodies
उत्तर
I1 < I2
In the given case, we have
MOI
\[\propto\] Density
The density of iron is more; therefore, I2 will be greater.
APPEARS IN
संबंधित प्रश्न
Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
The oxygen molecule has a mass of 5.30 × 10–26 kg and a moment of inertia of 1.94×10–46 kg m2 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.
(Hint: The moment of inertia of the door about the vertical axis at one end is ML2/3.)
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction µs = 0.25.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
A body having its centre of mass at the origin has three of its particles at (a,0,0), (0,a,0), (0,0,a). The moments of inertia of the body about the X and Y axes are 0⋅20 kg-m2 each. The moment of inertia about the Z-axis
Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not.
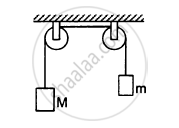
The pulleys shown in the following figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
The pulley shown in the following figure has a radius 10 cm and moment of inertia 0⋅5 kg-m2about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4⋅0 kg block.
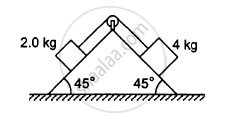
Solve the previous problem if the friction coefficient between the 2⋅0 kg block and the plane below it is 0⋅5 and the plane below the 4⋅0 kg block is frictionless.
A wheel of moment of inertia 0⋅500 kg-m2 and radius 20⋅0 cm is rotating about its axis at an angular speed of 20⋅0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
A wheel of moment of inertia 0⋅10 kg-m2 is rotating about a shaft at an angular speed of 160 rev/minute. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with a common angular speed of 200 rev/minute. Find the moment of inertia of the second wheel.
Two blocks of masses 400 g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has a moment of inertia \[1 \cdot 6 \times {10}^{- 4} kg - m^2\] and a radius 2⋅0 cm, Find (a) the kinetic energy of the system as the 400 g block falls through 50 cm, (b) the speed of the blocks at this instant.
Four bodies of masses 2 kg, 3 kg, 4 kg and 5 kg are placed at points A, B, C, and D respectively of a square ABCD of side 1 metre. The radius of gyration of the system about an axis passing through A and perpendicular to plane is
From a circular ring of mass ‘M’ and radius ‘R’ an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR2’. Then the value of ‘K’ is ______.
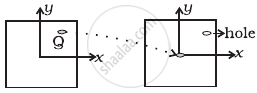
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind (Figure). The moment of inertia about the z-axis is then ______.
Moment of inertia (M.I.) of four bodies, having same mass and radius, are reported as :
I1 = M.I. of thin circular ring about its diameter,
I2 = M.I. of circular disc about an axis perpendicular to disc and going through the centre,
I3 = M.I. of solid cylinder about its axis and
I4 = M.I. of solid sphere about its diameter.
Then -
Consider a badminton racket with length scales as shown in the figure.
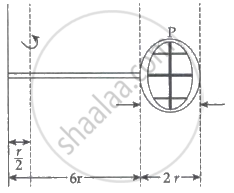
If the mass of the linear and circular portions of the badminton racket is the same (M) and the mass of the threads is negligible, the moment of inertia of the racket about an axis perpendicular to the handle and in the plane of the ring at, `r/2` distance from the ends A of the handle will be ______ Mr2.
