Advertisements
Advertisements
प्रश्न
A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.
(Hint: The moment of inertia of the door about the vertical axis at one end is ML2/3.)
उत्तर
Mass of the bullet, m = 10 g = 10 × 10–3 kg
Velocity of the bullet, v = 500 m/s
Thickness of the door, L = 1 m
Radius of the door, `r = 1/2 m`
Mass of the door, M = 12 kg
The Angular momentum imparted by the bullet on the door:
α = mvr
`=(10xx10^(-3))xx(500)xx1/2 = 2.5 kg m^2s^(-1)` ...(i)
Moment of inertia of the door:
`I = 1/3 ML^(2)`
`= 1/3 xx 12 xx (1)^2 = 4 kgm^2`
But `alpha = Iomega`
`:.omega = alpha/I`
`= 2.5/4 = 0.625 rad S^(-1)`
APPEARS IN
संबंधित प्रश्न
Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction µs = 0.25.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is ___________ .
Suppose the smaller pulley of the previous problem has its radius 5⋅0 cm and moment of inertia 0⋅10 kg-m2. Find the tension in the part of the string joining the pulleys.
The descending pulley shown in the following figure has a radius 20 cm and moment of inertia 0⋅20 kg-m2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1⋅0 kg.
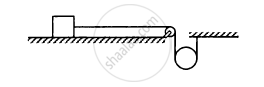
The pulley shown in the following figure has a radius 10 cm and moment of inertia 0⋅5 kg-m2about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4⋅0 kg block.
A diver having a moment of inertia of 6⋅0 kg-m2 about an axis thorough its centre of mass rotates at an angular speed of 2 rad/s about this axis. If he folds his hands and feet to decrease the moment of inertia to 5⋅0 kg-m2, what will be the new angular speed?
A boy is seated in a revolving chair revolving at an angular speed of 120 revolutions per minute. Two heavy balls form part of the revolving system and the boy can pull the balls closer to himself or may push them apart. If by pulling the balls closer, the boy decreases the moment of inertia of the system from 6 kg-m2 to 2 kg-m2, what will be the new angular speed?
A thin circular plate of mass M and radius R has its density varying as ρ(r) = ρ0r with ρ0 as constant and r is the distance from its center. The moment of Inertia of the circular plate about an axis perpendicular to the plate and passing through its edge is I = a MR2. The value of the coefficient a is ______.
