Advertisements
Advertisements
प्रश्न
Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
उत्तर १
`7/5 MR^2`
The moment of inertia (M.I.) of a sphere about its diameter = `2/5 MR^2`
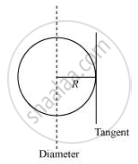
`ML = 2/5MR^2`
According to the theorem of parallel axes, the moment of inertia of a body about any axis is equal to the sum of the moment of inertia of the body about a parallel axis passing through its centre of mass and the product of its mass and the square of the distance between the two parallel axes.
The M.I. about a tangent of the sphere = `2/5 MR^2 + MR^2 = 7/5 MR^2`
उत्तर २
Moment of inertia of sphere about any diameter = 2/5 MR2
Applying theorem of parallel axes, Moment of inertia of sphere about a tangent to the sphere = 2/5MR2 +M(R)2 =7/5 MR2
APPEARS IN
संबंधित प्रश्न
A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5 m/s.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ω1 and ω2 are brought into contact face to face with their axes of rotation coincident. (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take ω1 ≠ ω2.
Let I1 an I2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminium and the second of iron.
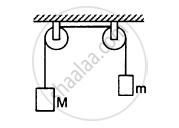
The pulleys shown in the following figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
Solve the previous problem if the friction coefficient between the 2⋅0 kg block and the plane below it is 0⋅5 and the plane below the 4⋅0 kg block is frictionless.
A wheel of moment of inertia 0⋅500 kg-m2 and radius 20⋅0 cm is rotating about its axis at an angular speed of 20⋅0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
A wheel of moment of inertia 0⋅10 kg-m2 is rotating about a shaft at an angular speed of 160 rev/minute. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with a common angular speed of 200 rev/minute. Find the moment of inertia of the second wheel.
Moment of inertia (M.I.) of four bodies, having same mass and radius, are reported as :
I1 = M.I. of thin circular ring about its diameter,
I2 = M.I. of circular disc about an axis perpendicular to disc and going through the centre,
I3 = M.I. of solid cylinder about its axis and
I4 = M.I. of solid sphere about its diameter.
Then -
Consider a badminton racket with length scales as shown in the figure.
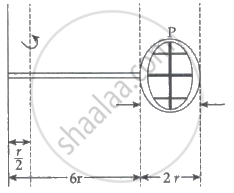
If the mass of the linear and circular portions of the badminton racket is the same (M) and the mass of the threads is negligible, the moment of inertia of the racket about an axis perpendicular to the handle and in the plane of the ring at, `r/2` distance from the ends A of the handle will be ______ Mr2.
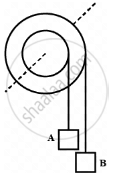
The figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then ______.