Advertisements
Advertisements
प्रश्न
Solve the previous problem if the friction coefficient between the 2⋅0 kg block and the plane below it is 0⋅5 and the plane below the 4⋅0 kg block is frictionless.
उत्तर
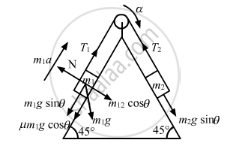
From the figure, we have
\[m_2 gsin\theta - T_2 = m_1 a..........(1)\]
\[ T_1 - \left( m_1 g\sin\theta + \mu m_1 g\cos \theta \right) = m_1 a ............(2)\]
\[ T_2 - T_1 = \frac{Ia}{r^2} .............(3)\]
Adding equations (1) and (2), we get
\[m_2 g\sin\theta - \left( m_1 g\sin\theta - \mu m_1 g\cos \theta \right) + \left( T_1 - T_2 \right) = m_1 a + m_2 a\]
\[m_2 g\sin\theta - \left( m_1 g\sin\theta + \mu m_1 g\cos \theta \right) - \frac{Ia}{r^2} = m_1 a + m_2 a\]
\[ m_2 g\sin\theta - \left( m_1 g\sin\theta + \mu m_1 g\cos \theta \right) = m_1 a + m_2 a + \frac{Ia}{r^2}\]
\[4 \times 9 . 8 \times \frac{1}{\sqrt{2}} - \left\{ 2 \times 9 . 8 \times \frac{1}{\sqrt{2}} + 0 . 5 \times 2 \times 9 . 8 \times \frac{1}{\sqrt{2}} \right\} = \left( 4 + 2 + \frac{0 . 5}{0 . 01} \right)a\]
\[ \Rightarrow 27 . 80 - 13 . 90 + 6 . 95 = 56a\]
\[ \Rightarrow 27 . 8 - 20 . 8 = 56a\]
\[ \Rightarrow a = \frac{7}{56} = 0 . 125 m/s^2\]
APPEARS IN
संबंधित प्रश्न
Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
The oxygen molecule has a mass of 5.30 × 10–26 kg and a moment of inertia of 1.94×10–46 kg m2 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5 m/s.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.
(Hint: The moment of inertia of the door about the vertical axis at one end is ML2/3.)
A body having its centre of mass at the origin has three of its particles at (a,0,0), (0,a,0), (0,0,a). The moments of inertia of the body about the X and Y axes are 0⋅20 kg-m2 each. The moment of inertia about the Z-axis
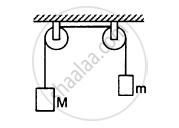
The pulleys shown in the following figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
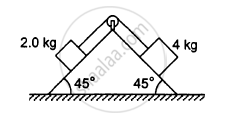
The pulley shown in the following figure has a radius 10 cm and moment of inertia 0⋅5 kg-m2about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4⋅0 kg block.
A boy is seated in a revolving chair revolving at an angular speed of 120 revolutions per minute. Two heavy balls form part of the revolving system and the boy can pull the balls closer to himself or may push them apart. If by pulling the balls closer, the boy decreases the moment of inertia of the system from 6 kg-m2 to 2 kg-m2, what will be the new angular speed?
A wheel of moment of inertia 0⋅10 kg-m2 is rotating about a shaft at an angular speed of 160 rev/minute. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with a common angular speed of 200 rev/minute. Find the moment of inertia of the second wheel.
A kid of mass M stands at the edge of a platform of radius R which can be freely rotated about its axis. The moment of inertia of the platform is I. The system is at rest when a friend throws a ball of mass m and the kid catches it. If the velocity of the ball is \[\nu\] horizontally along the tangent to the edge of the platform when it was caught by the kid, find the angular speed of the platform after the event.
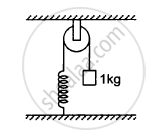
The pulley shown in the following figure has a radius of 20 cm and moment of inertia 0⋅2 kg-m2. The string going over it is attached at one end to a vertical spring of spring constant 50 N/m fixed from below, and supports a 1 kg mass at the other end. The system is released from rest with the spring at its natural length. Find the speed of the block when it has descended through 10 cm. Take g = 10 m/s2.
A wheel of mass 15 kg has a moment of inertia of 200 kg-m2 about its own axis, the radius of gyration will be:
From a circular ring of mass, ‘M’ and radius ‘R’ an arc corresponding to a 90° sector is removed. The moment of inertia of the remaining part of the ring about an axis passing through the centre of the ring and perpendicular to the plane of the ring is ‘K’ times ‘MR2’. Then the value of ‘K’ is ______.
Moment of inertia (M.I.) of four bodies, having same mass and radius, are reported as :
I1 = M.I. of thin circular ring about its diameter,
I2 = M.I. of circular disc about an axis perpendicular to disc and going through the centre,
I3 = M.I. of solid cylinder about its axis and
I4 = M.I. of solid sphere about its diameter.
Then -
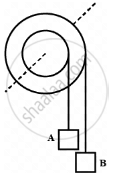
The figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then ______.