Advertisements
Advertisements
प्रश्न
A body having its centre of mass at the origin has three of its particles at (a,0,0), (0,a,0), (0,0,a). The moments of inertia of the body about the X and Y axes are 0⋅20 kg-m2 each. The moment of inertia about the Z-axis
विकल्प
is 0⋅20 kg-m2
is 0⋅40 kg-m2
is \[0 \cdot 20\sqrt{2}\]kg-m2
cannot be deduced with this information
उत्तर
cannot be deduced with this information
Ix = m2a2 + m3a2 = 0.20 ......(1)
Iy = m1a2 + m3a2 = 0.20 ......(2)
Iz = m1a2 + m2a2 ......(3)
We have three equations and four variables. So, Iz cannot be deduced with the given information.
APPEARS IN
संबंधित प्रश्न
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
A child stands at the centre of a turntable with his two arms outstretched. The turntable is set rotating with an angular speed of 40 rev/min. How much is the angular speed of the child if he folds his hands back and thereby reduces his moment of inertia to 2/5 times the initial value? Assume that the turntable rotates without friction.
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction µs = 0.25.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is ___________ .
The pulley shown in the following figure has a radius 10 cm and moment of inertia 0⋅5 kg-m2about its axis. Assuming the inclined planes to be frictionless, calculate the acceleration of the 4⋅0 kg block.
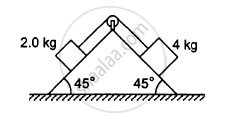
Solve the previous problem if the friction coefficient between the 2⋅0 kg block and the plane below it is 0⋅5 and the plane below the 4⋅0 kg block is frictionless.
A wheel of moment of inertia 0⋅500 kg-m2 and radius 20⋅0 cm is rotating about its axis at an angular speed of 20⋅0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
A wheel of moment of inertia 0⋅10 kg-m2 is rotating about a shaft at an angular speed of 160 rev/minute. A second wheel is set into rotation at 300 rev/minute and is coupled to the same shaft so that both the wheels finally rotate with a common angular speed of 200 rev/minute. Find the moment of inertia of the second wheel.
A wheel of mass 15 kg has a moment of inertia of 200 kg-m2 about its own axis, the radius of gyration will be:
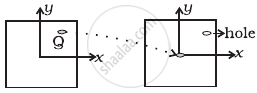
A uniform square plate has a small piece Q of an irregular shape removed and glued to the centre of the plate leaving a hole behind (Figure). The moment of inertia about the z-axis is then ______.
With reference to figure of a cube of edge a and mass m, state whether the following are true or false. (O is the centre of the cube.)
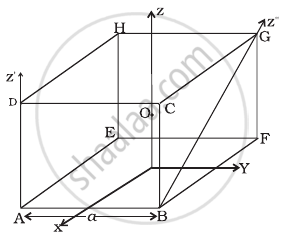
- The moment of inertia of cube about z-axis is Iz = Ix + Iy
- The moment of inertia of cube about z ′ is I'z = `I_z + (ma^2)/2`
- The moment of inertia of cube about z″ is = `I_z + (ma^2)/2`
- Ix = Iy
Why does a solid sphere have smaller moment of inertia than a hollow cylinder of same mass and radius, about an axis passing through their axes of symmetry?
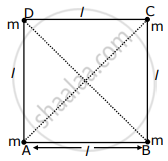
Four equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be ______.
Consider a badminton racket with length scales as shown in the figure.
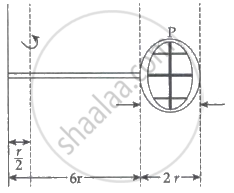
If the mass of the linear and circular portions of the badminton racket is the same (M) and the mass of the threads is negligible, the moment of inertia of the racket about an axis perpendicular to the handle and in the plane of the ring at, `r/2` distance from the ends A of the handle will be ______ Mr2.
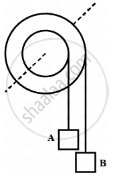
The figure shows a small wheel fixed coaxially on a bigger one of double the radius. The system rotates about the common axis. The strings supporting A and B do not slip on the wheels. If x and y be the distances travelled by A and B in the same time interval, then ______.
A thin circular plate of mass M and radius R has its density varying as ρ(r) = ρ0r with ρ0 as constant and r is the distance from its center. The moment of Inertia of the circular plate about an axis perpendicular to the plate and passing through its edge is I = a MR2. The value of the coefficient a is ______.
