Advertisements
Advertisements
प्रश्न
The oxygen molecule has a mass of 5.30 × 10–26 kg and a moment of inertia of 1.94×10–46 kg m2 about an axis through its centre perpendicular to the lines joining the two atoms. Suppose the mean speed of such a molecule in a gas is 500 m/s and that its kinetic energy of rotation is two thirds of its kinetic energy of translation. Find the average angular velocity of the molecule.
उत्तर १
Mass of an oxygen molecule, m = 5.30 × 10–26 kg
Moment of inertia, I = 1.94 × 10–46 kg m2
Velocity of the oxygen molecule, v = 500 m/s
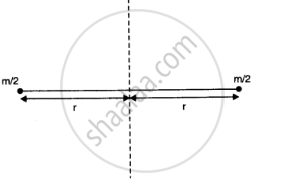
The separation between the two atoms of the oxygen molecule = 2r
Mass of each oxygen atom = `m/2`
Hence, moment of inertia I, is calculated as:
`(m/2)r^2 + (m/2)r^2 = mr^2`
r = `sqrt(I/m)`
`sqrt((1.94 xx 10^(-46))/(5.36 xx 10^(-26))) = 0.60 xx 10^(-10)m`
It is given that:
`KE_"rot" = KE_"trans`"`
`1/2 Iomega^2 =2/3 xx 1/2 "mv"^2`
`mr^2 omega^2 = 2/3 mv^2`
`omega = sqrt(2/3) v/r`
`= sqrt(2/3) xx 500/(0.6 xx 10^(-10))`
`= 6.80 xx 10^12 "rad/s"`
उत्तर २
`m = 5.30 xx 10^(-26)`
`I = 1.94 xx 10^(-46) kg m^2`
`v = 500 "m/s"`
if m/2 si mass of each of oxygen and 2r is distnace between the two atoms as shown in figure then.
`I = m/2 r^2 + m/2r^2 = mr^2`
`r = sqrt(I/m) = sqrt((1.94 xx 10^(-46))/(5.30 xx 10^(-26)))`
`= 0.61 xx 10^(-10) m`
As K.E of rotation = 2/3 K.E of transalation
`:. 1/2 Iomega^2 = 2/3 xx 1/2 momega^2`
`1/2(mr^2)omega^2 = 1/2 mv^2`
`omega = sqrt(2/3) v/r = sqrt(2/3) xx500 /(0.61xx10^(-10)) = 6.7 xx 10^(12) "rad/s"`
APPEARS IN
संबंधित प्रश्न
Find the moment of inertia of a sphere about a tangent to the sphere, given the moment of inertia of the sphere about any of its diameters to be 2MR2/5, where M is the mass of the sphere and R is the radius of the sphere.
A bullet of mass 10 g and speed 500 m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0 m wide and weighs 12 kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.
(Hint: The moment of inertia of the door about the vertical axis at one end is ML2/3.)
A cylinder of mass 10 kg and radius 15 cm is rolling perfectly on a plane of inclination 30°. The coefficient of static friction µs = 0.25.
(a) How much is the force of friction acting on the cylinder?
(b) What is the work done against friction during rolling?
(c) If the inclination θ of the plane is increased, at what value of θ does the cylinder begin to skid, and not roll perfectly?
The moment of inertia of a uniform semicircular wire of mass M and radius r about a line perpendicular to the plane of the wire through the centre is ___________ .
Let I1 an I2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminium and the second of iron.
Suppose the smaller pulley of the previous problem has its radius 5⋅0 cm and moment of inertia 0⋅10 kg-m2. Find the tension in the part of the string joining the pulleys.
The pulleys shown in the following figure are identical, each having a radius R and moment of inertia I. Find the acceleration of the block M.
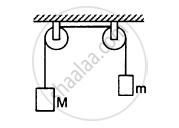
Two blocks of masses 400 g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has a moment of inertia \[1 \cdot 6 \times {10}^{- 4} kg - m^2\] and a radius 2⋅0 cm, Find (a) the kinetic energy of the system as the 400 g block falls through 50 cm, (b) the speed of the blocks at this instant.
With reference to figure of a cube of edge a and mass m, state whether the following are true or false. (O is the centre of the cube.)
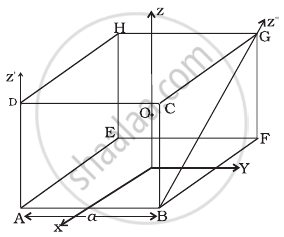
- The moment of inertia of cube about z-axis is Iz = Ix + Iy
- The moment of inertia of cube about z ′ is I'z = `I_z + (ma^2)/2`
- The moment of inertia of cube about z″ is = `I_z + (ma^2)/2`
- Ix = Iy
Why does a solid sphere have smaller moment of inertia than a hollow cylinder of same mass and radius, about an axis passing through their axes of symmetry?
