Advertisements
Advertisements
प्रश्न
Suppose the smaller pulley of the previous problem has its radius 5⋅0 cm and moment of inertia 0⋅10 kg-m2. Find the tension in the part of the string joining the pulleys.
उत्तर
Given
m = 2 kg, I1 = 0.10 kg-m2
r1 = 5 cm = 0.05 m
I2 = 2.20 kg-m2
r2 = 10 cm = 0.1 m
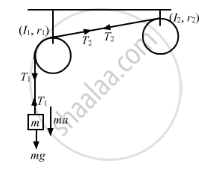
From the free body diagram, we have
\[mg - T_1 = ma....(1)\]
\[\left( T_1 - T_2 \right) r_1 = I_1 \alpha......(2)\]
\[ T_2 r_2 = I_2 \alpha .......(3)\]
Substituting the value of T2 in the equation (2), we get
\[\Rightarrow \left( T_1 - I_2 \frac{\alpha}{r_2} \right) r_1 = I_1 \alpha\]
\[ \Rightarrow T_1 - I_2 \frac{a}{r_2^2} = I_1 \frac{a}{r_1^2}\]
\[ \Rightarrow T_1 = \left\{ \left( \frac{I_1}{r_1^2} \right) + \left( \frac{I_2}{r_2^2} \right) \right\}a\]
Substituting the value of T1 in the equation (1), we get
\[mg - \left\{ \left( \frac{I_1}{r_1^2} \right) + \left( \frac{I_2}{r_2^2} \right) \right\}a = ma\]
\[\Rightarrow \frac{mg}{\left\{ \left( \frac{I_1}{r_1^2} \right) + \left( \frac{I_2}{r_2^2} \right) \right\} + m} = a\]
\[ \Rightarrow a = \frac{2 \times 9 . 8}{\frac{0 . 1}{0 . 0025} + \frac{0 . 2}{0 . 01} + 2}\]
\[= 0 . 316 m/s^2 \]
\[ \Rightarrow T_2 = I_2 \frac{a}{r_2^2}\]
\[ = \frac{0 . 20 \times 0 . 316}{0 . 01} = 6 . 32 N\]
APPEARS IN
संबंधित प्रश्न
Given the moment of inertia of a disc of mass M and radius R about any of its diameters to be MR2/4, find its moment of inertia about an axis normal to the disc and passing through a point on its edge
Torques of equal magnitude are applied to a hollow cylinder and a solid sphere, both having the same mass and radius. The cylinder is free to rotate about its standard axis of symmetry, and the sphere is free to rotate about an axis passing through its centre. Which of the two will acquire a greater angular speed after a given time?
A rope of negligible mass is wound round a hollow cylinder of mass 3 kg and radius 40 cm. What is the angular acceleration of the cylinder if the rope is pulled with a force of 30 N? What is the linear acceleration of the rope? Assume that there is no slipping.
A hoop of radius 2 m weighs 100 kg. It rolls along a horizontal floor so that its centre of mass has a speed of 20 cm/s. How much work has to be done to stop it?
A solid cylinder rolls up an inclined plane of angle of inclination 30°. At the bottom of the inclined plane, the centre of mass of the cylinder has a speed of 5 m/s.
(a) How far will the cylinder go up the plane?
(b) How long will it take to return to the bottom?
Two discs of moments of inertia I1 and I2 about their respective axes (normal to the disc and passing through the centre), and rotating with angular speeds ω1 and ω2 are brought into contact face to face with their axes of rotation coincident. (a) What is the angular speed of the two-disc system? (b) Show that the kinetic energy of the combined system is less than the sum of the initial kinetic energies of the two discs. How do you account for this loss in energy? Take ω1 ≠ ω2.
Let I1 an I2 be the moments of inertia of two bodies of identical geometrical shape, the first made of aluminium and the second of iron.
A body having its centre of mass at the origin has three of its particles at (a,0,0), (0,a,0), (0,0,a). The moments of inertia of the body about the X and Y axes are 0⋅20 kg-m2 each. The moment of inertia about the Z-axis
A string is wrapped on a wheel of moment of inertia 0⋅20 kg-m2 and radius 10 cm and goes through a light pulley to support a block of mass 2⋅0 kg as shown in the following figure. Find the acceleration of the block.
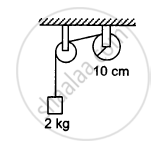
Solve the previous problem if the friction coefficient between the 2⋅0 kg block and the plane below it is 0⋅5 and the plane below the 4⋅0 kg block is frictionless.
A wheel of moment of inertia 0⋅500 kg-m2 and radius 20⋅0 cm is rotating about its axis at an angular speed of 20⋅0 rad/s. It picks up a stationary particle of mass 200 g at its edge. Find the new angular speed of the wheel.
A diver having a moment of inertia of 6⋅0 kg-m2 about an axis thorough its centre of mass rotates at an angular speed of 2 rad/s about this axis. If he folds his hands and feet to decrease the moment of inertia to 5⋅0 kg-m2, what will be the new angular speed?
Two blocks of masses 400 g and 200 g are connected through a light string going over a pulley which is free to rotate about its axis. The pulley has a moment of inertia \[1 \cdot 6 \times {10}^{- 4} kg - m^2\] and a radius 2⋅0 cm, Find (a) the kinetic energy of the system as the 400 g block falls through 50 cm, (b) the speed of the blocks at this instant.
A wheel of mass 15 kg has a moment of inertia of 200 kg-m2 about its own axis, the radius of gyration will be:
With reference to figure of a cube of edge a and mass m, state whether the following are true or false. (O is the centre of the cube.)
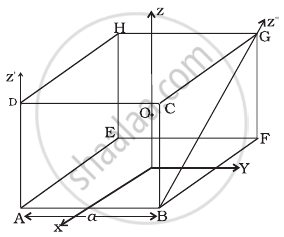
- The moment of inertia of cube about z-axis is Iz = Ix + Iy
- The moment of inertia of cube about z ′ is I'z = `I_z + (ma^2)/2`
- The moment of inertia of cube about z″ is = `I_z + (ma^2)/2`
- Ix = Iy
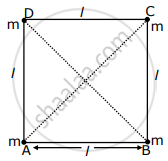
Four equal masses, m each are placed at the corners of a square of length (l) as shown in the figure. The moment of inertia of the system about an axis passing through A and parallel to DB would be ______.
A thin circular plate of mass M and radius R has its density varying as ρ(r) = ρ0r with ρ0 as constant and r is the distance from its center. The moment of Inertia of the circular plate about an axis perpendicular to the plate and passing through its edge is I = a MR2. The value of the coefficient a is ______.
