Advertisements
Advertisements
Question
A square coil of side 30 cm with 500 turns is kept in a uniform magnetic field of 0.4 T. The plane of the coil is inclined at an angle of 30° to the field. Calculate the magnetic flux through the coil.
Solution
Square coil of side (a) = 30 cm = 30 × 10-2m
Area of square coil (A) = a2 = (30 × 10-2)2 = 9 × 10-2 m2
Number of turns (N) = 500
Magnetic field (B) = 0.4 T
Angular between the field and coil (θ) = 90 – 30 = 60°
Magnetic flux (Φ) = NBA cos 0
= 500 × 0.4 × 9 × 10-2 × cos 60° = 18 × 12
Φ = 9 W b
APPEARS IN
RELATED QUESTIONS
A rectangular wire loop of sides 8 cm and 2 cm with a small cut is moving out of a region of uniform magnetic field of magnitude 0.3 T directed normal to the loop. What is the emf developed across the cut if the velocity of the loop is 1 cm s−1 in a direction normal to the
- longer side,
- shorter side of the loop?
For how long does the induced voltage last in each case?
The magnetic flux through a loop is varying according to a relation `phi = 6t^2 + 7t + 1` where `phi` is in milliweber and t is in second. What is the e.m.f. induced in the loop at t = 2 second?
If ‘R’ is the radius of dees and ‘B’ be the magnetic field of induction in which positive charges (q) of mass (m) escape from the cyclotron, then its maximum speed (vmax) is _______.
A) `(qR)/(Bm)`
B)`(qm)/(Br)`
C) `(qBR)/m`
D) `m/(qBR)`
Explain why, an electromagnet is called a temporary magnet.
A coil has a self-inductance of 0·05 Henry. Find the magnitude of the emf induced in it when the current flowing through it is changing at the rate of 100 As-1.
A 50 cm long solenoid has 400 turns per cm. The diameter of the solenoid is 0.04 m. Find the magnetic flux linked with each turn when it carries a current of 1 A.
A coil of 200 turns carries a current of 0.4 A. If the magnetic flux of 4 mWb is linked with each turn of the coil, find the inductance of the coil.
What should be the core of an electromagnet?
A conducting bar of length L is free to slide on two parallel conducting rails as shown in the figure
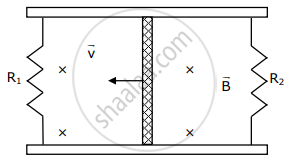
Two resistors R1 and R2 are connected across the ends of the rails. There is a uniform magnetic field `vec"B"` pointing into the page. An external agent pulls the bar to the left at a constant speed v. The correct statement about the directions of induced currents I1 and I2 flowing through R1 and R2 respectively is:
Show that for a given positive ion species in a cyclotron, (i) the radius of their circular path inside a dee is directly proportional to their speed, and (ii) the maximum ion energy achievable is directly proportional to the square of the magnetic induction.
