Advertisements
Advertisements
Question
A square of side L meters lies in the x-y plane in a region, where the magnetic field is given by `B = Bo(2hati + 3hatj + 4hatk)`T, where B0 is constant. The magnitude of flux passing through the square is ______.
Options
`2 B_0 L^2 Wb`
`3 B_0 L^2 Wb`
`4 B_0 L^2 Wb`
`sqrt(29) B_0 L^2 Wb`
Solution
A square of side L meters lies in the x-y plane in a region, where the magnetic field is given by `B = Bo(2hati + 3hatj + 4hatk)`T, where B0 is constant. The magnitude of flux passing through the square is `underline(4 B_0 L^2 Wb`).
Explanation:
Magnetic flux is defined as the total number of magnetic lines of force passing normally through an area placed in a magnetic field and is equal to the magnetic flux linked with that area.
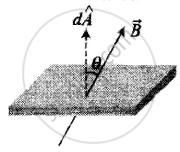
For elementary area dA of a surface flux linked `dphi = BdA cos theta` or `dphi = vecB*dvecA`
So, Net flux through the surface `phi = oint vecB xx dvecA = BA cos theta`
In this problem, `A = L^2 hatk` and `B = B_0 (2hati + 3hatj + 4hatk)T`
`phi - vecB.vecA = B_0 (2hati + 3hatj + 4hatk) * L^2 hatk = 4B_0L^2 Wb`
APPEARS IN
RELATED QUESTIONS
A pair of adjacent coils has a mutual inductance of 1.5 H. If the current in one coil changes from 0 to 20 A in 0.5 s, what is the change of flux linkage with the other coil?
A rectangular coil having 60 turns and area of 0.4m2 is held at right angles to a uniform magnetic field of flux density 5 × 10-5T. Calculate the magnetic flux passing through it.
A metallic loop is placed in a nonuniform magnetic field. Will an emf be induced in the loop?
An inductor is connected to a battery through a switch. Explain why the emf induced in the inductor is much larger when the switch is opened as compared to the emf induced when the switch is closed.
Find magnetic flux density at a point on the axis of a long solenoid having 5000 tums/m when it carrying a current of 2 A.
The magnetic flux linked with a coil of N turns of area of cross-section A held with its plane parallel to the field B is ______.
Two inductors of inductance L each are connected in series with the opposite? magnetic fluxes. The resultant inductance is ______.
The magnetic flux linked with a coil in Wb is given by the equation Φ = 3t2 + 4t + 9. Then the magnitude of induced emf at t = 2 sec will be ______.
A coil is placed in a time varying magnetic field. If the number of turns in the coil were to be halved and the radius of wire doubled, the electrical power dissipated due to the current induced in the coil would be: (Assume the coil to be short circuited.)
