Advertisements
Advertisements
Question
A steel tape 1m long is correctly calibrated for a temperature of 27.0 °C. The length of a steel rod measured by this tape is found to be 63.0 cm on a hot day when the temperature is 45.0 °C. What is the actual length of the steel rod on that day? What is the length of the same steel rod on a day when the temperature is 27.0 °C? Coefficient of linear expansion of steel = 1.20 × 10–5 K–1
Solution 1
On a day when the temperature is 27 °C, the length of 1 cm division on the steel tape is exactly 1 cm, because the tape has been calibrated for 27 °C.When the temperature rises to 45 °C (that is, ΔT = 45 – 27 = 18 °C), the increase in the length of 1 cm division is Δl = αlΔT = (1.2 x 10-5C-1) x 1 cm x 18 °C = 0.000216 cm Therefore, the length of 1 cm division on the tape becomes 1.000216 cm at 45 °C. As the length of the steel rod is read to be 63.0 cm on the steel tape at 45 °C, the actual length of the rod at 45 °C is 63.0 x 1.000216 cm = 63.0136 cm The length of the same rod at 27 °C is 63.0 cm, because 1 cm mark on the steel tape is exactly 1 cm at 27 °C.
Solution 2
Length of the steel tape at temperature T = 27°C, l = 1 m = 100 cm
At temperature T1 = 45°C, the length of the steel rod, l1 = 63 cm
Coefficient of linear expansion of steel, α = 1.20 × 10–5 K–1
Let l2 be the actual length of the steel rod and l' be the length of the steel tape at 45°C.
`l' = l + al(T-1- T)`
`:. l' = 100 + 1.20 xx 10^(-5) xx 100(45- 27)`
= 100.0216 cm
Hence, the actual length of the steel rod measured by the steel tape at 45°C can be calculated as:
`l_2= 100.0216/100 xx 63 = 63.0136 cm`
Therefore, the actual length of the rod at 45.0°C is 63.0136 cm. Its length at 27.0°C is 63.0 cm.
APPEARS IN
RELATED QUESTIONS
A gas thermometer measures the temperature from the variation of pressure of a sample of gas. If the pressure measured at the melting point of lead is 2.20 times the pressure measured at the triple point of water, find the melting point of lead.
An iron plate has a circular hole of a diameter 11 cm. Find the diameter of the hole when the plate is uniformly heated from 10° C to 90° C.`[alpha = 12 xx 10^-6//°"C"]`
A metal rod of Young's moduls 'Y' and coefficient of linear expansion 'a' has its temeprature raised by 'Δ θ'. The linear stress to prevent the expansion of rod is ______.
(L and l is original length of rod and expansion respectively)
An aluminium sphere is dipped into water. Which of the following is true?
A student records the initial length l, change in temperature ∆T and change in length ∆l of a rod as follows:
| S.No. | l(m) | ∆T (C) | ∆l (m) |
| 1. | 2 | 10 | `4 xx 10^-4` |
| 2. | 1 | 10 | `4 xx 10^-4` |
| 3. | 2 | 20 | `2 xx 10^-4` |
| 4. | 3 | 10 | `6 xx 10^-4` |
If the first observation is correct, what can you say about observations 2, 3 and 4.
Find out the increase in moment of inertia I of a uniform rod (coefficient of linear expansion α) about its perpendicular bisector when its temperature is slightly increased by ∆T.
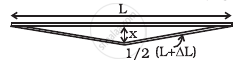
A rail track made of steel having length 10 m is clamped on a raillway line at its two ends (figure). On a summer day due to rise in temperature by 20° C, it is deformed as shown in figure. Find x (displacement of the centre) if αsteel = 1.2 × 10–5/°C.
The height of mercury column measured with brass scale at temperature T0 is H0. What height H' will the mercury column have at T = 0°C. Coefficient of volume expansion of mercury is γ. Coefficient of linear expansion of brass is α ______.
A metal ball immersed in water weighs w1 at 0°C and w2 at 50°C. The coefficient of cubical expansion of metal is less than that of water. Then ______.
A metal rod Y = 2 × 1012 dyne cm-2 of coefficient of linear expansion 1.6 × 10-5 per °C has its temperature raised by 20°C. The linear compressive stress to prevent the expansion of the rod is ______.
