Question

A stone of mass m is tied to an elastic string of negligble mass and spring constant k. The unstretched length of the string is L and has negligible mass. The other end of the string is fixed to a nail at a point P. Initially the stone is at the same level as the point P. The stone is dropped vertically from point P.

1. Find the distance y from the top when the mass comes to rest for an instant, for the first time.
2. What is the maximum velocity attained by the stone in this drop?
3. What shall be the nature of the motion after the stone has reached its lowest point?

Answer 1

Consider the diagram the stone is dropped from point p.

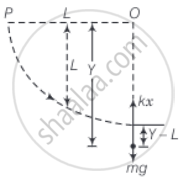
a. Till the stone drops through a length Z it will be in free fall. After that, the elasticity of the string will force it to an SHM. Let the stone come to rest instantaneously at y.

The loss in PE of the stone is the PE stored in the stretched string.

`mgy = 1/2 k(y - L)^2`

⇒ `mgy = 1/2 ky^2 - kyL + 1/2 kL^2`

⇒ `1/2 ky^2 - (kL + mg)y + 1/2 kL^2` = 0

`y = ((kL + mg) +- sqrt((kL + mg)^2 - k^2L^2))/k`

= `((kL  + mg) +- sqrt(2mgkL + m^2g^2))/k`

Retain the positive sign,

∴ `y = ((kLmg) sqrt(mgkL + m^2g^2))/k`

b. In SHM, the maximum velocity is attained when the body passes, through the “equilibrium, position” ie., when the instantaneous acceleration is zero. That is mg – kx = 0, where x is the extension from L.

⇒ `mg = kx`

Let the velocity be v. Then,

= `1/2 mv^21/22 kx^2 = mg(L + x)`  .....(From the conservation of energy)

= `1/2 mv^2 = mg (L + x) - 1/2 kx^2`

Now, `mg = kx`

⇒ `x = (mg)/k`

∴ `1/2 mv^2 = mg(L + (mg)/k) - 1/2 k (m^2g^2)/k^2` 

= `mgL + (m^2g^2)/k - 1/2 (m^2g^2)/k`

`1/2 mv^2 =  mgL + 1/2 (m^2g^2)/k`

∴ `v^2 = 2gL + (mg^2)/k`

`v^2 = (2gL + (mg^2)/k)^(1/2)`

c. When the stone is at the lowest position i.e., at instantaneous distance Y from P, then the equation of motion of the stone is `(md^2y)/(dt^2) = mg - k(y - L)`

⇒ `(d^2y)/(dt^2) + k/m (y - L) - g` = 0

Make a transformation of variables, `z = k/m (y - L) - g`

∴ `(d^2z)/(dt^2) + k/m z` = 0

It is a differential equation of second order  which represents SHM

Comparing with equation `(d^2z)/(dt^2) + omega^2z` = 0

Angular frequency of harmonic motion `omega = sqrt(k/m)`

The solution of the above equation will be of the type z = `A cos (omega t + phi)`, where `omega = sqrt(k/m)`

`y = (L + (mg)/k) + A^' cos (omegat + pi)`

Thus, the stone will perform SHM with angular frequency `omega = sqrt(k/m)` about a point `y_0 = L + (mg)/k`.