Advertisements
Advertisements
Question
A tank open at the top is made of iron sheet 4 m wide. If the dimensions of the tank are 12 m × 8 m × 6 m, find the cost of iron sheet at Rs 17.50 per metre.
Solution
\[\text { An open iron tank of dimensions 12 m } \times 8 m \times 6 m is \text { to be made . }\]
\[\text { Surface area of the open tank = (area of the base) + (total area of the 4 walls) }\]
\[ = (12 \times 8) + 2 \times (8 \times 6 + 12 \times 6)\]
\[ = (96) + 2 \times (48 + 72)\]
\[ = 336 m^2 \]
\[\text { Also, it is given that the cost of the iron sheet that is 4 m wide is Rs 17 . 50 per metre } . \]
\[\text { i . e . , the area of the iron sheet = 1 m }\times 4 m = 4 m^2 \]
\[\text { So, the cost of 4 }m^2 \text { of iron sheet = Rs 17 . 50 }\]
\[ \therefore \text { The cost of iron sheet required to an iron tank of surface area 336 } m^2 = 336 \times \frac{17 . 50}{4} = Rs 1470\]
APPEARS IN
RELATED QUESTIONS
Find the lateral surface area and total surface area of a cuboid of length 80 cm, breadth 40 cm and height 20 cm.
Ravish wanted to make a temporary shelter for his car by making a box-like structure with tarpaulin that covers all the four sides and the top of the car ( with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m with
base dimensions 4 m × 3m?
Find the volume in cubic metre (cu. m) of the cuboid whose dimensions is length = 12 m, breadth = 10 m, height = 4.5 cm.
A rectangular water reservoir contains 105 m3 of water. Find the depth of the water in the reservoir if its base measures 12 m by 3.5 m.
Three cubes of metal whose edges are in the ratio 3 : 4 : 5 are melted down in to a single cube whose diagonal is 12 `sqrt(3)` cm. Find the edges of three cubes.
The surface area of a cuboid is 1300 cm2. If its breadth is 10 cm and height is 20 cm2, find its length.
Find the curved surface area and the total surface area of a right circular cylinder whose height is 15 cm and the diameter of the cross-section is 14 cm.
The length and breadth of a cuboid are 20 cm and 15 cm respectively. If its volume is 2400 cm3, find its height.
375 persons can be accommodated in a room whose dimensions are in the ratio of 6 : 4 : 1. Calculate the area of the four walls of the room if the each person consumes 64m3 of air.
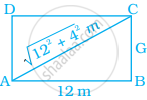
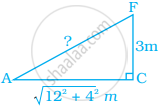
Find the length of the largest pole that can be placed in a room of dimensions 12 m × 4 m × 3 m.