Advertisements
Advertisements
Question
Answer the following question.
A thin circular ring of radius r is charged uniformly so that its linear charge density becomes λ. Derive an expression for the electric field at a point P at a distance x from it along the axis of the ring. Hence, prove that at large distances (x >> r), the ring behaves as a point charge.
Solution
Let consider a thin circular ring of radius r with charge density as `lambda`
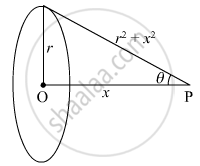
We need to find the electric field due to this charged ring at a point on the axis of the ring at a distance x from its centre.
Let us consider a small charge element `(dx)` on the ring having small charge `dq`
`dq = lambdadx`
the electric field due to this charge element at the point P is given by
`d"E" = 1/(4piepsilon_0) (dq)/((r^2+x^2)`
`d"E" = 1/(4piepsilon_0) (lambda dx)/((r^2+x^2)`
Electric field at the point P will have two components one in the vertical direction and the other one in the horizontal direction.
`d E cos theta` along the horizontal direction.
`d E sin theta` along the vertical direction.
The vertical components will cancel out the effect of each other due to the presence of the diametrically opposite element.
So the horizontal component of the electric field will survive at the point P.
From the figure we have the value of `cos theta = x/sqrt(r^2+x^2)`
Now the integration of the horizontal component `dE cos theta` will be carried out.
`dE cos theta = (lambdax dx)/(4piepsilon_0(r^2+x^2)3/2`
Since the value of `dq = lambda dx`
`dE cos theta = (xdq)/(4piepsilon_0(r^2+x^2)3/2`
Now integrating the above equation and taking x and r quantities as constants we get
`E_x = int_ dE cos theta = int_ (xdx)/(4piepsilon_0(r^2+x^2)3/2`
`E_x = int_ (xdq)/(4piepsilon_0(r^2+x^2)3/2) = (x"Q")/(4piepsilon_0(r^2+x^2)3/2` where Q is the total charge on the ring.
Here `E_x` is the value of the total electric field at the point P
Special case:
when x >> r, the denominator of the above equation gets modified in the following way:
`r^2 + x^2 ≈ x^2`
`E_x = (x"Q")/(4piepsilon_0(x^2)3/2) = (x"Q")/(4piepsilon_0x^3) = ("Q")/(4piepsilon_0x^2)`
So at large distances (x >> r), the ring behaves as a point charge.
APPEARS IN
RELATED QUESTIONS
A copper wire of radius 0.1 mm and resistance kΩ is connected across a power supply of 20 V. (a) How many electrons are transferred per second between the supply and the wire at one end? (b) Write down the current density in the wire.
Which of the following statements is false?
Two parallel large thin metal sheets have equal surface densities 26.4 x 10-12 C/m2 of opposite signs. The electric field between these sheets is ______.
A battery is connected to the conductor of non-uniform cross section area. The quantities or quantity which remains constant is ______.
A copper wire of length 1 m and radius 1 mm is joined in series with an iron wire of length 2 m and radius 3 mm and a current is passed through the wires. The ratio of current densities in the copper and iron wires is ______
Column: I give certain physical terms associated with the flow of current through a metallic conductor.
Column: II gives some mathematical relations involving electrical quantities.
Match Column I and Column II with appropriate relations.
| Column - I | Column - II | ||
| (A) | Drift Velocity | (P) | `"m"/("ne"^2ρ)` |
| (B) | Electrical Resistivity | (Q) | `"neν"_"d"` |
| (C) | Relaxation Period | (R) | `"eE"/"m"τ` |
| (D) | Current Density | (S) | `"E"/"J"` |
Column - I gives certain physical terms associated with flow of current through a metallic conductor. Column - II gives some mathematical relations involving electrical quantities. Match Column - I and Column - II with appropriate relations.
| Column - I | Column - II | ||
| (A) | Drift Velocity | (P) | `"m"/("ne"^2ρ)` |
| (B) | Electrical Resistivity | (Q) | `"ne"υ_"d"` |
| (c) | Relaxation Period | (R) | `("eE")/"m"τ` |
| (D) | Current Density | (S) | `"E"/"J"` |
