Advertisements
Advertisements
Question
A truck starts from rest and accelerates uniformly at 2.0 m s–2. At t = 10 s, a stone is dropped by a person standing on the top of the truck (6 m high from the ground).
- What are the velocity, and
- acceleration of the stone at t = 11?(Neglect air resistance.)
Solution
u = 0, a = 2 ms-2, t 10 s
Using equation, v = u + at, we get
v = 0 + 2 x 10 = 20 ms-1
(a) Initial velocity of the truck, u = 0
Acceleration, a = 2 m/s2
Time, t = 10 s
As per the first equation of motion, final velocity is given as:
v = u + at
= 0 + 2 × 10 = 20 m/s
The final velocity of the truck and hence, of the stone is 20 m/s.
At t = 11 s, the horizontal component (vx) of velocity, in the absence of air resistance, remains unchanged, i.e.,
vx = 20 m/s
The vertical component of the stone's velocity (vy) is calculated using the first equation of motion as:
vy = u + ayδt
Where, δt = 11 – 10 = 1 s and ay = g = 10 m/s2
∴vy = 0 + 10 × 1 = 10 m/s
The resultant velocity (v) of the stone is given as:
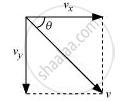
v = `sqrt(v_x^2+v_y^2)`
`= sqrt(20^2 + 10^2) = sqrt(400 + 100)`
=`sqrt(500)` = 22.36 m/s
Let 𝜃 represent the angle that the resultant velocity forms with the horizontal component of velocity,vx
`∴ tan theta = (v_y)/(v_x)`
`theta = tan^(-1)(10)/(20)`
`=tan^(-1)(0.5)`
= `26.57^@`
(b) When the stone is released from the truck, there are no horizontal forces acting on it. Nonetheless, the stone still moves due to gravity. Therefore, the stone's acceleration is 10 m/s², directed vertically downward.
APPEARS IN
RELATED QUESTIONS
One end of a string of length l is connected to a particle of mass m and the other to a small peg on a smooth horizontal table. If the particle moves in a circle with speed the net force on the particle (directed towards the centre) is:
T is the tension in the string.
A body of mass 5 kg is acted upon by two perpendicular forces 8 N and 6 N. Give the magnitude and direction of the acceleration of the body.
Explain why a horse cannot pull a cart and run in empty space.
In Figure, the co-efficient of friction between the floor and the body B is 0.1. The co-efficient of friction between the bodies B and A is 0.2. A force F is applied as shown on B. The mass of A is m /2 and of B is m. Which of the following statements are true?

- The bodies will move together if F = 0.25 mg.
- The body A will slip with respect to B if F = 0.5 mg.
- The bodies will move together if F = 0.5 mg.
- The bodies will be at rest if F = 0.1 mg.
- The maximum value of F for which the two bodies will move together is 0.45 mg.
Mass m1 moves on a slope making an angle θ with the horizontal and is attached to mass m2 by a string passing over a frictionless pulley as shown in figure. The coefficient of friction between m1 and the sloping surface is µ.

- If m2 > m1 sin θ, the body will move up the plane.
- If m2 > m1 (sin θ + µ cos θ), the body will move up the plane.
- If m2 < m1 (sin θ + µ cos θ), the body will move up the plane.
- If m2 < m1 (sin θ − µ cos θ), the body will move down the plane.
Why are mountain roads generally made winding upwards rather than going straight up?
Two masses of 5 kg and 3 kg are suspended with help of massless inextensible strings as shown in figure. Calculate T1 and T2 when whole system is going upwards with acceleration = 2 ms2 (use g = 9.8 ms–2).

A block of mass M is held against a rough vertical wall by pressing it with a finger. If the coefficient of friction between the block and the wall is µ and the acceleration due to gravity is g, calculate the minimum force required to be applied by the finger to hold the block against the wall?
A person in an elevator accelerating upwards with an acceleration of 2 ms–2, tosses a coin vertically upwards with a speed of 20 ms1. After how much time will the coin fall back into his hand? ( g = 10 ms–2)
A rectangular box lies on a rough inclined surface. The co-efficient of friction between the surface and the box is µ. Let the mass of the box be m.
- At what angle of inclination θ of the plane to the horizontal will the box just start to slide down the plane?
- What is the force acting on the box down the plane, if the angle of inclination of the plane is increased to α > θ ?
- What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed?
- What is the force needed to be applied upwards along the plane to make the box move up the plane with acceleration a?
