Advertisements
Advertisements
Question
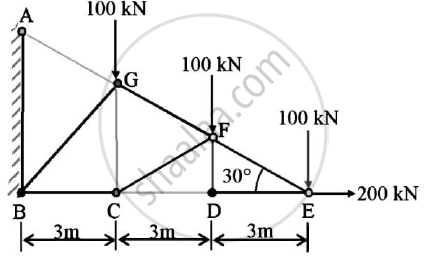
A truss is loaded and supported as shown.Determine the following:
(1)Identify the zero force members,if any
(2)Find the forces in members EF,ED and FC by method of joints.
(3)Find the forces in members GF,GC and BC by method of sections
Solution
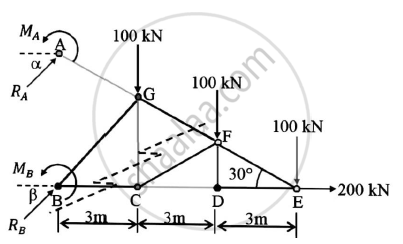
By analysis of truss,we can say that DE is zero force member
METHOD OF JOINTS:
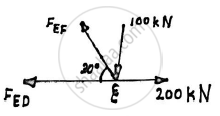
Joint E:
Applying the conditions of equilibrium
ΣFY=0
FEFsin30-100=0
FEF=200 kN
Applying the conditions of equilibrium
ΣFX=0
-FEFcos30-FED+200=0
-200cos30+200=FED
FED=26.7949 kN
△FED is congruent to △FCD
∠FCD=∠FED=30°
JOINT F:
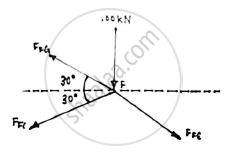
Applying the conditions of equilibrium
ΣFY=0
FFGsin30-FFCsin30-FFEsin30-100=0
FFG-FFC-200=200
FFG-FFC=400 ……….(1)
ΣFX=0
-FFGcos30-FFCcos30+FFEcos30=0
Dividing by cos30
FFG +FFC = 200 ………(2)
Solving (1) and (2)
FFG=300 kN
FFC=-100 kN
METHOD OF SECTIONS:
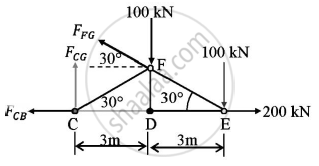
In △FED
tan 30 = `(FD)/(DE)`
DE=3m
FD=`sqrt(3)` m
Consider the equilibrium of the truss section
ΣMC=0
FFGcos 30 x FD + FFGsin30 x CD -100 x CD -100 X CE = 0
3FFG=900
FFG=300 kN
Applying the conditions of equilibrium
ΣFX=0
-FFGcos30-FcB+200=0
-300cos30+200=FcB
FcB=-59.8076 kN
ΣFY=0
FcG+FFGsin30-100-100=0
FcG=50 kN
| Member of truss | Magnitude of force(kN) | Nature of force |
| BC | 59.8076 | Compression |
| GC | 50 | Tension |
| GF | 300 | Tension |
| FC | 100 | Compression |
| ED | 26.7949 | Tension |
| EF | 200 | Tension |
APPEARS IN
RELATED QUESTIONS
Referring to the truss shown in the figure. Find :
(a) Reaction at D and C
(b)Zero force members.
(c)Forces in member FE and DC by method of section.
(d)Forces in other members by method of joints.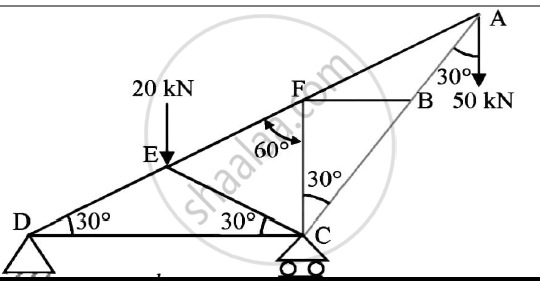
What is a zero force member in a truss? With examples state the conditions for a zero force member.
In the truss shown in figure,compute the forces in each member.