Question

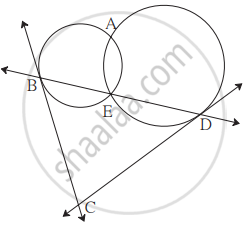
दो वृत्त परस्पर बिंदु A तथा बिंदु E पर प्रतिच्छेदित करते हैं। बिंदु E से खींची गई सामान्य छेदन रेखा वृत्तों को बिंदु B तथा बिंदु D पर प्रतिच्छेदित करती है। बिंदु B तथा बिंदु D से खींची गई स्पर्श रेखाएँ परस्पर बिंदु C पर प्रतिच्छेदित करती हैं। सिद्ध कीजिए कि, `square`ABCD एक चक्रीय चतुर्भुज है।

 

Answer 1

रेख AB, रेख AE और रेख AD खींचों |

∴ `{:(∠"EBC" = ∠"BAE", ........(1)),(∠"EDC" = ∠"DAE", ........(2)):}}` ...........(स्पर्श रेखा-छेदन रेखा के प्रमेय से)

ΔBCD में,

∠DBC + ∠BDC + ∠BCD = 180° .....(त्रिभुज के सभी कोणों के मापों का योग)

∠EBC + ∠EDC + ∠BCD = 180° ........(B-E-D)

∴ ∠BAE + ∠DAE + ∠BCD = 180° ..........[(1) और (2) से]

∴ (∠BAE + ∠DAE) + ∠BCD = 180°

∴ ∠BAD + ∠BCD = 180° ..........(कोणों के मापों का योग गुणधर्म)

∴ `square`ABCD एक चक्रीय चतुर्भुज है। ..........(चक्रीय चतुर्भुज के प्रमेय का विलोम)