Advertisements
Advertisements
Question
A uniform metre rule of weight 10 gf is pivoted at its 0 mark.
- What moment of force depresses the rule?
- How can it be made horizontal by applying a least force?
Solution
Weight of metre scale = 10 gf
- Moment of force = 10 × 50 cm = 500 gf cm
- It can be made horizontal by a moment of force = 500 gf cm
500 = w × 100
∴ w = `500/100`
= 5 gf cm
By applying 5 gf upward at the 100 cm mark.
APPEARS IN
RELATED QUESTIONS
Describe a simple experiment to verify the principle of moments, if you are supplied with a metre rule, a fulcrum and two springs with slotted weights.
A uniform metre rule is pivoted at its mid-point. A weight of 50 gf is suspended at one end of it. Where should a weight of 100 gf be suspended to keep the rule horizontal?
The diagram below shows a uniform bar supported at the middle point O. A weight of 40 gf is placed at a distance of 40 cm to the left of the point O. How can you balance the bar with a weight of 80 gf?
When a boy weighing 20 kgf sits at one end of a 4 m long see-saw, it gets depressed at this end. How can it be brought to the horizontal position by a man weighing 40 kgf.
A uniform metre rule of mass 100 g is balanced on the fulcrum at mark 40 cm by suspending an unknown mass m at the mark 20 cm.
- Find the value of m.
- To which side the rule will tilt if the mass m is moved to the mark 10 cm?
- What is the resultant moment now?
- How can it be balanced by another mass of 50 g?
A uniform metre rule balances horizontally on a knife edge placed at the 58 cm mark when a weight of 20 gf is suspended from one end.
- Draw a diagram of the arrangement.
- What is the weight of the rule?
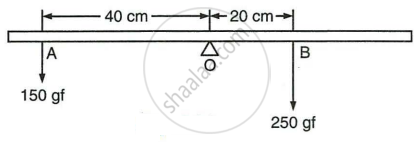
The diagram in Fig. shows a uniform metre rule weighing 100 gf, pivoted at its centre O. Two weights 150 gf and 250 gf hang from the point A and B respectively of the metre rule such that OA = 40 cm and OB = 20 cm. Calculate :
- the total anticlockwise moment about O,
- the total clockwise moment about O,
- the difference of anticlockwise and clockwise moments, and
- the distance from O where a 100 gf weight should be placed to balance the metre rule.
A uniform half-metre rule can be balanced at the 29.0 cm mark when a mass of 20 g is hung from its one end.
- Draw a diagram of the arrangement.
- Find the mass of the half-metre rule.
- In which direction would the balancing point shift if 20 g mass is shifted inside from its one end?
A uniform metre rule of mass 100g is balanced on a fulcrum at mark 40cm by suspending an unknown mass m at the mark 20cm.
How can it be balanced by another mass 50 g ?
State the principle of moments.
