Advertisements
Advertisements
Question
A uniform metre scale can be balanced at the 70.0 cm mark when a mark when a mass 0.05 kg is hung from the 94.0 cm mark
1) draw a diagram of the arrangement
2) Find the mass of the metre scale
Solution
1) Diagram of the given arrangement is shown below.
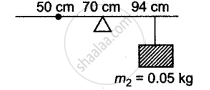
2) As the given meter scale is a uniform scale. So its centre of gravity lies at 50 cm. Let the mass of the meter-scale be W1 kg.
From the principle of moments
Anticlockwise moment = clockwise moment
m1x1 = m2x2
m1 × (70 − 50) = 0.05 × (94 − 70)
m1 = `(0.05xx24)/20`
= 0.06 kg.
= 60 gm.
APPEARS IN
RELATED QUESTIONS
Less force is needed when applied at a farther distance from the pivoted point.
State two effects of a force when applied on a body.
A potter turns his wheel by applying a force through the stick near the rim of wheel.
Sleepers are used below the rails.
State Newton's Second law of motion. Under what conditon does it take the form F = ma?
Name of S.I. unit of momentum.
State the relationship between force, mass and acceleration. Draw graphs showing the relationship between Acceleration and mass for a constant force.
What do you understand by the clockwise and anticlockwise moment of force? When is it taken positive?
The diagram shows a uniform metre rule weighing 100gf, pivoted at its centre O. Two weights 150gf and 250gf hang from the point A and B respectively of the metre rule such that OA = 40 cm and OB = 20 cm. Calculate :
the difference of anticlockwise and clockwise moment
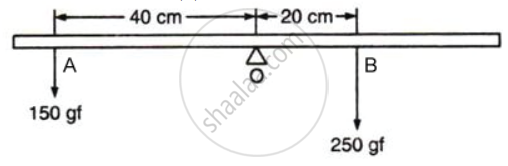
State two factors on which moment of the force about a point depends.
