Advertisements
Advertisements
Question
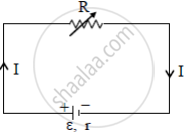
A variable resistor R is connected across a cell of emf ε and internal resistance r as shown in the figure. Draw a plot showing the variation of
(i) Terminal voltage V and
(ii) the current I, as a function of R.
Solution
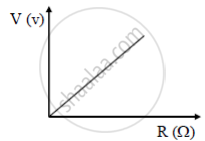
(i) Terminal voltage across a cell as a function of R
As resistance R increases current (I) in the circuit decreases and terminal voltage (V) increases.
We know V = ε –Ir; Where ε is emf of the cell
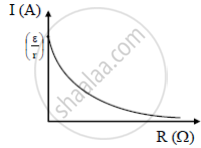
(ii) Current I as a function of R.
The current across a cell is given by `"I" = epsilon/("R"+"r")`
When R increases I decreases
APPEARS IN
RELATED QUESTIONS
A heating element using nichrome connected to a 230 V supply draws an initial current of 3.2 A which settles after a few seconds to a steady value of 2.8 A. What is the steady temperature of the heating element if the room temperature is 27.0°C? The temperature coefficient of resistance of nichrome averaged over the temperature range involved is 1.70 × 10−4 °C−1.
Consider a circuit containing an ideal battery connected to a resistor. Do "work done by the battery" and "the thermal energy developed" represent two names of the same physical quantity?
A non-ideal battery is connected to a resistor. Is work done by the battery equal to the thermal energy developed in the resistor? Will your answer change if the battery is ideal?
Sometimes it is said that "heat is developed" in a resistance when there is an electric current in it. Recall that heat is defined as the energy being transferred due to temperature difference. Is the statement in quotes technically correct?
As temperature increases, the viscosity of liquids decreases considerably. Will this decrease the resistance of an electrolyte as the temperature increases?
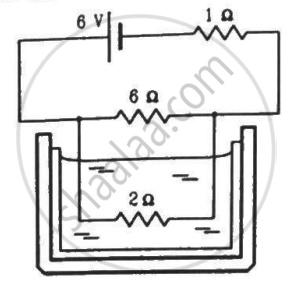
The 2.0 Ω resistor shown in the figure is dipped into a calorimeter containing water. The heat capacity of the calorimeter together with water is 2000 J K−1. (a) If the circuit is active for 15 minutes, what would be the rise in the temperature of the water? (b) Suppose the 6.0 Ω resistor gets burnt. What would be the rise in the temperature of the water in the next 15 minutes?
A metallic wire has a resistance of 3.0 Ω at 0°C and 4.8 Ω at 150°C. Find the temperature coefficient of resistance of its material.
Water at 10°C enters into a geyser. The water drawn out from the geyser has a temperature of 60°C and the rate of outflow of water is 18 kg/hr. The rating of the geyser is :
The specific resistance of all the metals is the most affected by ______
