Advertisements
Advertisements
Question
Sometimes it is said that "heat is developed" in a resistance when there is an electric current in it. Recall that heat is defined as the energy being transferred due to temperature difference. Is the statement in quotes technically correct?
Solution
Yes, the given statement is correct. When charge flows through a conductor, its electric potential energy decreases. This loss in electric potential energy appears as increased heat energy of the resistor. Thus, heat energy is developed in a resistor when there is an electric current in it.
APPEARS IN
RELATED QUESTIONS
The order of coloured rings in a carbon resistor is red, yellow, blue and silver. The resistance of the
carbon resistor is:
a) 24 x 106 Ω ± 5%
b) 24 x 106 Ω ± 10%
c) 34 x 104 Ω ± 10%
d) 26 x 104 Ω ± 5%
Show variation of resistivity of Si with temperature in a graph ?
The thermal energy developed in a current-carrying resistor is given by U = i2 Rt and also by U = Vit. Should we say that U is proportional to i2 or i?
Consider a circuit containing an ideal battery connected to a resistor. Do "work done by the battery" and "the thermal energy developed" represent two names of the same physical quantity?
Is work done by a battery always equal to the thermal energy developed in electrical circuit? What happens if a capacitor is connected in the circuit?
The resistance of an iron wire and a copper wire at 20°C are 3.9 Ω and 4.1 Ω, respectively. At what temperature will the resistance be equal? Temperature coefficient of resistivity for iron is 5.0 × 10–3 K–1 and for copper, it is 4.0 × 10–3 K–1. Neglect any thermal expansion.
When a current passes through a resistor, its temperature increases. Is it an adiabatic process?
Is neutral temperature always the arithmetic mean of the inversion temperature and the temperature of the cold junction? Does the unit of temperature have an effect in deciding this question?
An electric kettle used to prepare tea, takes 2 minutes to boil 4 cups of water (1 cup contains 200 cc of water) if the room temperature is 25°C. (a) If the cost of power consumption is Re 1.00 per unit (1 unit = 1000 watt-hour), calculate the cost of boiling 4 cups of water. (b) What will be the corresponding cost if the room temperature drops to 5°C?
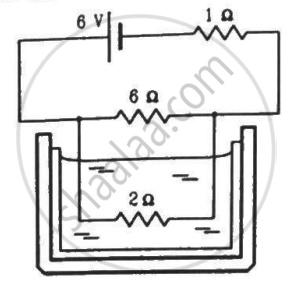
The 2.0 Ω resistor shown in the figure is dipped into a calorimeter containing water. The heat capacity of the calorimeter together with water is 2000 J K−1. (a) If the circuit is active for 15 minutes, what would be the rise in the temperature of the water? (b) Suppose the 6.0 Ω resistor gets burnt. What would be the rise in the temperature of the water in the next 15 minutes?
Find the thermo-emf developed in a copper-silver thermocouple when the junctions are kept at 0°C and 40°C. Use the data given in the following table.
| Metal with lead (Pb) |
a `mu V"/"^oC` |
b `muV"/("^oC)` |
| Aluminium | -0.47 | 0.003 |
| Bismuth | -43.7 | -0.47 |
| Copper | 2.76 | 0.012 |
| Gold | 2.90 | 0.0093 |
| Iron | 16.6 | -0.030 |
| Nickel | 19.1 | -0.030 |
| Platinum | -1.79 | -0.035 |
| Silver | 2.50 | 0.012 |
| Steel | 10.8 | -0.016 |
A carbon resistor has coloured bands as shown in Figure 2 below. The resistance of the resistor is:
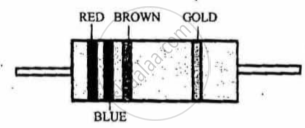
figure 2
A metallic wire has a resistance of 3.0 Ω at 0°C and 4.8 Ω at 150°C. Find the temperature coefficient of resistance of its material.
By increasing the temperature, the specific resistance of a conductor and a semiconductor -
The higher and lower fixed points on a thermometer are separated by 160 mm. When the length of the mercury thread above the lower point is 40 mm, the temperature reading would be :
Temperature dependence of resistivity ρ(T) of semiconductors, insulators and metals is significantly based on the following factors:
- number of charge carriers can change with temperature T.
- time interval between two successive collisions can depend on T.
- length of material can be a function of T.
- mass of carriers is a function of T.
The temperature (T) dependence of resistivity of materials A and material B is represented by fig (i) and fig (ii) respectively. Identify material A and material B.
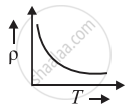 fig. (i) |
 fig. (ii) |
