Advertisements
Advertisements
Question
A wheel of radius 20 cm is pushed to move it on a rough horizontal surface. If is found to move through a distance of 60 cm on the road during the time it completes one revolution about the centre. Assume that the linear and the angular accelerations are uniform. The frictional force acting on the wheel by the surface is ______________________ .
Options
along the velocity of the wheel
opposite to the velocity of the wheel
perpendicular to the velocity of the wheel
zero
Solution
along the velocity of the wheel
As the distance covered in one revolution about the centre is less than the perimeter of the wheel, it means that the direction of torque due to frictional force opposes the motion of wheel, i.e., the frictional force acting on the wheel by the surface is along the velocity of the wheel.
Notes
Missing Figure in Answer
APPEARS IN
RELATED QUESTIONS
If the ice at the poles melts and flows towards the equator, how will it affect the duration of day-night?
A hollow sphere, a solid sphere, a disc and a ring all having same mass and radius are rolled down on an inclined plane. If no slipping takes place, which one will take the smallest time to cover a given length?
A closed cylindrical tube containing some water (not filling the entire tube) lies in a horizontal plane. If the tube is rotated about a perpendicular bisector, the moment of inertia of water about the axis __________ .
A cubical block of mass M and edge a slides down a rough inclined plane of inclination θ with a uniform velocity. The torque of the normal force on the block about its centre has a magnitude
The centre of a wheel rolling on a plane surface moves with a speed \[\nu_0\] A particle on the rim of the wheel at the same level as the centre will be moving at speed ___________ .
A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top of a smooth incline and released. Least time will be taken in reaching the bottom by _________ .
A solid sphere, a hollow sphere and a disc, all having same mass and radius, are placed at the top on an incline and released. The friction coefficients between the objects and the incline are same and not sufficient to allow pure rolling. Least time will be taken in reaching the bottom by ___________ .
In the previous question, the smallest kinetic energy at
the bottom of the incline will be achieved by ___________ .
A string of negligible thickness is wrapped several times around a cylinder kept on a rough horizontal surface. A man standing at a distance l from the cylinder holds one end of the string and pulls the cylinder towards him (see the following figure). There is no slipping anywhere. The length of the string passed through the hand of the man while the cylinder reaches his hands is _________ .
Consider a wheel of a bicycle rolling on a level road at a linear speed \[\nu_0\] (see the following figure)
(a) the speed of the particle A is zero
(b) the speed of B, C and D are all equal to \[v_0\]
(c) the speed of C is 2 \[v_0\]
(d) the speed of B is greater than the speed of O.

Three particles, each of mass 200 g, are kept at the corners of an equilateral triangle of side 10 cm. Find the moment of inertial of the system about an axis passing through one of the particles and perpendicular to the plane of the particles.

Particles of masses 1 g, 2 g, 3 g, .........., 100 g are kept at the marks 1 cm, 2 cm, 3 cm, ..........., 100 cm respectively on a metre scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the metre scale.
The moment of inertia of a uniform rod of mass 0⋅50 kg and length 1 m is 0⋅10 kg-m2about a line perpendicular to the rod. Find the distance of this line from the middle point of the rod.
Find the moment of inertia of a uniform square plate of mass m and edge a about one of its diagonals.
The surface density (mass/area) of a circular disc of radius a depends on the distance from the centre as [rholeft( r right) = A + Br.] Find its moment of inertia about the line perpendicular to the plane of the disc thorough its centre.
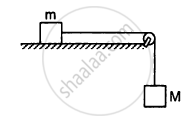
The following figure shows two blocks of mass m and M connected by a string passing over a pulley. The horizontal table over which the mass m slides is smooth. The pulley has a radius r and moment of inertia I about its axis and it can freely rotate about this axis. Find the acceleration of the mass M assuming that the string does not slip on the pulley.
A sphere of mass m rolls on a plane surface. Find its kinetic energy at an instant when its centre moves with speed \[\nu.\]
