Question

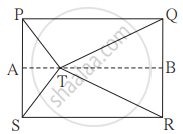
आकृती मध्ये दाखविल्यानुसार T हा बिंदू आयत PQRS च्या अंतर्भागात आहे, तर सिद्ध करा, TS² + TQ² = TP² + TR² (आकृतीत दाखवल्याप्रमाणे A-T-B असा रेख AB || बाजू SR काढा.)

Answer 1

पक्ष: `square`PQRS हा आयत आहे. बिंदू T हा आयत `square`PQRS च्या अंतर्भागात आहे. 

साध्य: TS² + TQ² = TP² + TR² 

रचना: रेख AB || बाजू SR असा काढा, की A-T-B.

सिद्धता:

`square`PQRS हा आयत आहे. ........[दिलेले]

∴ PS = QR ....(i) [आयताच्या संमुख बाजू]

`square`ASRB मध्ये

∠S = ∠R = 90°  ....(ii) [आयत PQRS चे कोन]

बाजू AB || बाजू SR ......[रचना]

तसेच, `{:(∠"A" = ∠"S" = 90°), (∠"B" = ∠"R" = 90°):}}` .....[दूरस्थ आंतरकोनाचे प्रमेय, (ii) वरून]

∴ ∠A = ∠B = ∠S = ∠R = 90°  ....(iii)

∴ `square`ASRB हा आयत आहे.

 

∴ AS = BR  .....(iv) [आयताच्या संमुख बाजू]

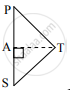
ΔPTS मध्ये, ∠PST हा लघुकोन आहे.

व रेख AT ⊥ बाजू PS  ......[(iii) वरून]

∴ TP² = PS² + TS² - 2PS.AS .....(v) [पायथागोरसच्या प्रमेयाचे उपयोजन]

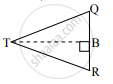
ΔTQR मध्ये, ∠TRQ हा लघुकोन आहे.

व रेख BT ⊥ बाजू QR  ......[(iii) वरून]

∴ TQ² = RQ² + TR² - 2RQ.BR ....(vi) [पायथागोरसच्या प्रमेयाचे उपयोजन]

TP² - TQ² = PS² + TS² - 2PS.AS - RQ² - TR² + 2RQ.BR .....[(v) मधून (vi) वजा करून]

∴ TP² - TQ² = TS² - TR² + PS² - RQ² - 2PS.AS + 2RQ.BR

∴ TP² - TQ² = TS² - TR² + PS² - PS² - 2PS.BR + 2PS.BR  .....[(i) व (iv) वरून]

∴ TP² - TQ² = TS² - TR²

∴ TS² + TQ² = TP² + TR²