Advertisements
Advertisements
Question
आकृती मध्ये रेख PS ही ΔPQR ची मध्यगा आहे आणि PT ⊥ QR तर सिद्ध करा,
(1) `"PR"^2 = "PS"^2 + "QR" xx "ST" + ("QR"/2)^2`
(2) `"PQ"^2 = "PS"^2 - "QR" xx "ST" + ("QR"/2)^2`

Solution
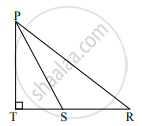
(1) QS = SR = `1/2`QR .....(i) [S हा बाजू QR चा मध्यबिंदू आहे.]
ΔPSR मध्ये, ∠PSR हा विशालकोन आहे ....[पक्ष]
व PT ⊥ SR ....[पक्ष, Q-S-R]
∴ PR2 = SR2 + PS2 + 2SR × ST .....(ii) [पायथागोरसच्या प्रमेयाचे उपयोजन]
∴ PR2 = `(1/2"QR")^2 + "PS"^2 + 2(1/2"QR") xx "ST"` ...[(i) व (ii) वरून]
∴ PR2 = `("QR"/2)^2 + "PS"^2 + "QR" xx "ST"`
∴ `"PR"^2 = "PS"^2 + "QR" xx "ST" + ("QR"/2)^2`
(2)
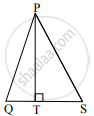
∴ ΔPQS मध्ये, ∠PSQ हा लघुकोन आहे ....[पक्ष]
PT ⊥ QS ......[पक्ष, Q-S-R]
∴ PQ2 = QS2 + PS2 - 2QS × ST ....(iii) [पायथागोरसच्या प्रमेयाचे उपयोजन]
∴ PQ2 = `(1/2"QR")^2 + "PS"^2 - 2(1/2"QR") xx "ST"` ....[(i) व (iii) वरून]
∴ PQ2 = `("QR"/2)^2 + "PS"^2 - "QR" xx "ST"`
∴ `"PQ"^2 = "PS"^2 - "QR" xx "ST" + ("QR"/2)^2`