Advertisements
Advertisements
Question
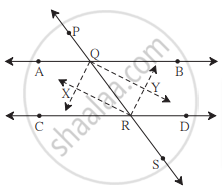
आकृती मध्ये रेषा AB || रेषा CD व रेषा PS ही त्यांची छेदिका आहे. किरण QX, किरण QY, किरण RX, किरण RY हे काेनदुभाजक आहेत, तर `square`QXRY हा आयत आहे हे दाखवा.
Solution
पक्ष: AB आणि CD या दोन समांतर रेषा आहेत ज्या अनुक्रमे Q आणि R बिंदूंवर छेदिका PS द्वारे कापल्या जातात. आतील कोनांचे दुभाजक X आणि Y बिंदूंना छेदतात.
साध्य: `square`QXRY हा आयत आहे.
सिद्धता: रेषा AB || रेषा CD व रेषा PS ही त्यांची छेदिका आहे.
∠AQR = ∠DRQ ...(आंतरव्युत्क्रम कोन)
⇒ `1/2` ∠AQR = `1/2`∠DRQ ...(1)
किरण QK हे ∠AQR चे दुभाजक आहे आणि किरण RK हे ∠DRQ चे दुभाजक आहे, तर
∠XQR = `1/2`∠AQR आणि ∠YRQ = `1/2`∠DRQ
∴ (1) वरून
∠XQR = ∠YRQ
∠XQR आणि ∠YRQ हे रेषा QR आणि छेदिका QX आणि RY द्वारे तयार झालेले आंतरव्युत्क्रम कोन आहेत.
∴ QX || RY ...(व्युत्क्रम कोन कसाेटी)
त्याचप्रमाणे, RX || QY.
म्हणून, `square`QXRY मध्ये, QX || आहे RY आणि RX || QY
ज्या चौकोनाच्या संमुख बाजूंच्या जोड्या एकरूप असतात तो चौकोन समांतरभुज असतो.
QXRY हे समांतरभुज आहे.
∠BQR + ∠DRQ = 180∘
⇒ `1/2` ∠BQR + `1/2` ∠DRQ = 90∘ ...(2)
किरण QY हे ∠BQR चे दुभाजक आहे आणि किरण RY हे ∠DRQ चे दुभाजक आहे, तर
∠YQR = `1/2`∠BQR आणि ∠YRQ = `1/2`∠DRQ
∴ (2) वरून
∠YQR + ∠YRQ = 90∘ ...(3)
∆QRY मध्ये,
∠YQR + ∠YRQ + ∠QYR = 180∘ ...(त्रिकोणाचे कोन बेरीज गुणधर्म)
⇒ 90∘ + ∠QYR = 180∘ ...[(3) वरून]
⇒ ∠QYR = 180∘ − 90∘
⇒ ∠QYR = 90∘
QXRY हे समांतरभुज चौकोन आहे, तर
∠QXR = ∠QYR ...(समांतरभुज चौकोनाचे संमुख कोन एकरूप असतात.)
⇒ ∠QXR = 90∘ ...(∵ ∠QYR = 90∘)
समांतरभुज चौकोनाचे लगतचे कोन पूरक असतात, तर
∠QXR + ∠XRY = 180∘
⇒ 90∘ + ∠XRY = 180∘ ...(∵ ∠QXR = 90∘)
⇒ ∠XRY = 180∘ − 90∘
⇒ ∠XRY = 90∘
∠XQY = ∠XRY = 90∘ ...(समांतरभुज चौकोनाचे संमुख कोन एकरूप असतात.)
अशा प्रकारे, QXRY हा एक समांतरभुज चौकोन आहे ज्याचे सर्व आंतरकोन काटकोन आहेत.
आयत हा एक समांतरभुज चौकोन आहे ज्यामध्ये प्रत्येक कोन काटकोन असतो.
∴ `square`QXRY हा आयत आहे.
APPEARS IN
RELATED QUESTIONS
आकृती मध्ये रेषा RP || रेषा MS व रेषा DK ही त्यांची छेदिका आहे. ∠DHP = 85°
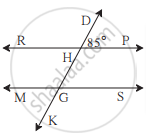
तर खालील कोनांची मापे काढा.
- ∠RHD
- ∠PHG
- ∠HGS
- ∠MGK
आकृती पाहा. रेषा p || रेषा q आणि रेषा l व रेषा m या छेदिका आहेत. काही काेनांची मापे दाखवली आहेत.
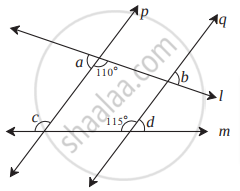
यावरून ∠a, ∠b, ∠c, ∠d यांची मापे काढा.
आकृती मध्ये रेषा l || रेषा m व रेषा n || रेषा p आहे.
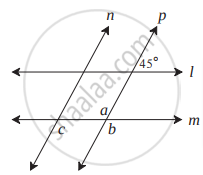
एका कोनाच्या दिलेल्या मापावरून ∠a, ∠b, ∠c ची मापे काढा.
आकृती मध्ये, ∠PQR आणि ∠XYZ यांच्या भुजा परस्परांना समांतर आहेत.
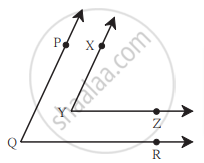
तर सिद्ध करा, की ∠PQR ≅ ∠XYZ.
आकृती मध्ये, रेषा AB || रेषा CD आणि रेषा PQ ही छेदिका आहे तर आकृतीत दाखवलेल्या कोनांच्या मापांवरून पुढील कोनांची मापे काढा.
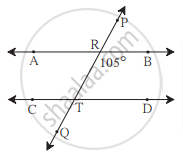
- ∠ART
- ∠CTQ
- ∠DTQ
- ∠PRB
आकृती मध्ये y = 108° आणि x = 71° तर रेषा m व रेषा n समांतर होतील का? कारण लिहा.
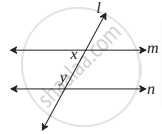
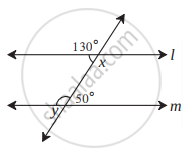
आकृती मध्ये दर्शवलेल्या कोनांच्या मापांवरून ∠x आणि ∠y यांची मापे काढा आणि सिद्ध करा की रेषा l || रेषा m.
आकृती मध्ये जर रेषा AB || रेषा CF आणि रेषा BC || रेषा ED तर सिद्ध करा ∠ABC = ∠FDE.