Advertisements
Advertisements
Question
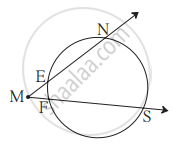
आकृति में m(चाप NS) = 125°, m(चाप EF) = 37°, तो ∠NMS का माप ज्ञात कीजिए।
Solution
m(चाप NS) = 125°, m(चाप EF) = 37° ........(दिया है)
∠NMS का शीर्षबिंदु M यह वृत्त बाह्य भाग में है | कोण की भुजाओं द्वारा चाप EF और चाप NS अंतःखंडित होता है |
∴ ∠NMS = `1/2`[m(चाप NS) - m(चाप EF)]
∴ ∠NMS = `1/2 xx [125^circ - 37^circ]`
∴ ∠NMS = `1/2 xx 88^circ`
∴ ∠NMS = 44°
∠NMS = 44°.
RELATED QUESTIONS
बाह्यस्पर्शी दो वृत्तों की त्रिज्याएँ क्रमशः 5.5 सेमी तथा 4.2 सेमी हों तो उनके केंद्रों के बीच की दूरी ज्ञात कीजिए।
4 सेमी और 2.8 सेमी त्रिज्या वाले (1) बाह्यस्पर्शी (2) अंतःस्पर्शी वृत्त बनाइए।
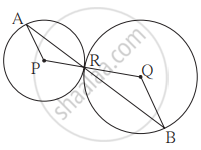
आकृति में P तथा Q केंद्र वाले वृत्त एकदूसरे को R बिंदु पर स्पर्श करते हैं। बिंदु R से जानेवाली रेखा उन वृत्तों को क्रमशः बिंदु A तथा बिंदु B पर प्रतिच्छेदित करती हो तो -
(1) सिद्ध कीजिए रेख AP || रेख BQ
(2) सिद्ध कीजिए ΔAPR ~ ΔRQB
(3) यदि ∠PAR का माप 35° हो, तो ∠RQB का माप ज्ञात कीजिए।
दिए गए प्रत्येक उप प्रश्न के लिए चार वैकल्पिक उत्तर दिए हैं। उनमें से उचित विकल्प चुनकर लिखिए।
परस्पर बाह्य स्पर्श करनेवाले दो वृत्तों में अधिक से अधिक कितनी स्पर्श रेखाएँ खींची जा सकती हैं?
दिए गए प्रत्येक उप प्रश्न के लिए चार वैकल्पिक उत्तर दिए हैं। उनमें से उचित विकल्प चुनकर लिखिए।
किसी वृत्त की जीवाएँ AB और CD परस्पर वृत्त के अंतर्भाग में बिंदु E पर प्रतिच्छेदित करती हैं। यदि AE = 5.6, EB = 10, CE = 8 तो ED = कितना?
