SSC (Hindi Medium)
Academic Year: 2023-2024
Date & Time: 15th March 2024, 11:00 am
Duration: 2h
Advertisements
सूचना -
- सभी प्रश्न हल करना अनिवार्य है।
- गणकयंत्र (कैल्कुलेटर) का उपयोग करना मना है।
- दाईं ओर के आँकड़े प्रश्नों के पूर्ण अंक दर्शाते हैं।
- प्रत्येक बहुपर्यायी प्रश्न (MCQ) के प्रथम प्रयास का ही मूल्यांकन होगा [जैसे Q. 1 (A)] तथा अंकदान होगा।
- जहाँ आवश्यक हो, वहाँ उत्तर के लिए उचित आकृतियाँ बनाइये।
- रचनाओं के सभी चिन्ह स्पष्ट होने चाहिए। उन्हें मिटाइये नहीं।
- प्रमेय की उपपत्ति लिखने के लिए आकृति आवश्यक है।
निम्नलिखित बहुवैकल्पिक प्रश्न के दिए गए उत्तरों में से उचित विकल्प चुनकर लिखिए।
निम्नलिखित में से कौन-से दिनांक की संख्या पायथागोरस का त्रिक् हैं?
15/08/17
16/08/16
3/5/17
4/9/15
Chapter: [0.02] पाइथागोरस का प्रमेय
नीचे दिए गए बहुवैकल्पिक प्रश्न के उत्तर का सही विकल्प चुनकर लिखिए।
sinθ cosecθ = कितना?
1
0
`1/2`
`sqrt2`
Chapter: [0.06] त्रिकोणमिति
X-अक्ष का ढाल = ?
1
-1
0
अपरिभाषित
Chapter: [0.05] निर्देशांक भूमिति
3 सेमी त्रिज्या वाले वृत्त की सबसे बड़ी जीवा लंबाई = ?
1.5 सेमी
3 सेमी
6 सेमी
9 सेमी
Chapter: [0.03] वृत्त
यदि Δ ABC और ~ Δ PQR और AB : PQ = 2 : 3 तो `(A(Δ "ABC"))/(A(Δ "PQR")` का मान ज्ञात कीजिए।
Chapter: [0.01] समरूपता
5 सेमी तथा 3 सेमी त्रिज्या वाले दो वृत्त परस्पर बाह्यस्पर्श करते हैं, तो उनके केंद्रों के बीच की दूरी ज्ञात कीजिए।
Chapter: [0.03] वृत्त
यदि वर्ग के विकर्ण की लंबाई 10`sqrt2` सेमी हो, तो उस वर्ग की भुजा की लंबाई ज्ञात कीजिए।
Chapter: [0.02] पाइथागोरस का प्रमेय
किसी रेखा द्वारा X-अक्ष की धन दिशा की ओर निर्मित कोण का माप दिया गया है, इस आधार पर रेखा का ढाल ज्ञात कीजिए।
45°
Chapter: [0.05] निर्देशांक भूमिति
Advertisements

ऊपर दी गयी आकृति में, ∠ABC यह चाप ABC में अंतर्लिखित कोण है।
यदि ∠ABC = 60%, तो m ∠AOC ज्ञात कीजिए।
हल:
∠ABC = `1/2`m (चाप AXC) ...... `square`
60° = `1/2` m (चाप AXC)
`square` = m (चाप AXC)
परंतु m ∠ AOC = m(चाप`square`) ......(केंद्रीय कोण का गुणधर्म)
∴ m ∠AOC = `square`
Chapter: [0.03] वृत्त
sin2θ + cos2θ का मान ज्ञात कीजिए।

हल:
Δ ABC में, ∠ABC = 90°, ∠C = θ°
AB2 + BC2 = `square` .....(पायथागोरस प्रमेय)
दोनों पक्षों में AC2 से भाग देने पर,
`"AB"^2/"AC"^2 + "BC"^2/"AC"^2 = "AC"^2/"AC"^2`
∴ `("AB"^2/"AC"^2) + ("BC"^2/"AC"^2) = 1`
परन्तु `"AB"/"AC" = square और "BC"/"AC" = square`
∴ `sin^2 theta + cos^2 theta = square`
Chapter: [0.06] त्रिकोणमिति
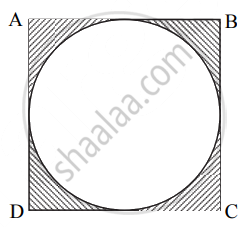
ऊपर दी गयी आकृति में `square`ABCD एक वर्ग है और एक वृत उसमें अंतर्लिखित है। वर्ग की सभी भुजायें वृत्त को स्पर्श करती हैं।
यदि AB = 14 सेमी, तो रेखांकित भाग का क्षेत्रफल ज्ञात कीजिए।
हल:
वर्ग का क्षेत्रफल = `(square)^2` ...(सूत्र)
= 142
= `square` वर्ग सेमी
∴ वृत्त का क्षेत्रफल = `square` ...(सूत्र)
= `22/7 xx 7 xx 7`
= 154 वर्ग सेमी
∴ रेखांकित भाग का क्षेत्रफल = (वर्ग का क्षेत्रफल) - (वृत्त का क्षेत्रफल)
= 196 - 154
= `square` वर्ग सेमी
Chapter: [0.07] महत्वमापन
किसी द्वैत्रिज्य की त्रिज्या 3.5 सेमी तथा उसके वृत्त चाप की लंबाई 2.2 सेमी हो तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
Chapter: [0.07] महत्वमापन
किसी समकोण त्रिभुज में समकोण बनाने वाली भुजाएँ क्रमश: 9 सेमी तथा 12 सेमी हों तो उस त्रिभुज के कर्ण की लंबाई ज्ञात कीजिए।
Chapter: [0.02] पाइथागोरस का प्रमेय
आकृति में m(चाप NS) = 125°, m(चाप EF) = 37°, तो ∠NMS का माप ज्ञात कीजिए।
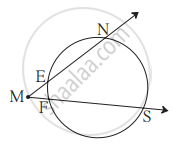
Chapter: [0.03] वृत्त
नीचे दिए गए बिंदुओं से होकर जानेवाली रेखा का ढाल ज्ञात कीजिए।
A (2, 3) और B (4, 7)
Chapter: [0.05] निर्देशांक भूमिति
किसी गोले की त्रिज्या 7 सेमी हो तो उसका पृष्ठफल ज्ञात कीजिए।
Chapter: [0.07] महत्वमापन
Advertisements

ΔABC में, किरण BD यह ∠ABC का कोण समद्विभाजक है। A - D - C, रेख DE || भुजा BC, A - E - B हो, तो सिद्ध कीजिए `("AB")/("BC") = ("AE")/("EB")`
उपपत्ति:
ΔABC में, किरण BD यह ∠B को समद्विभाजित करता है।
∴ `square/("BC") = ("AD")/("DC")` ......(I) (`square`)
ΔABC में, DE || BC
∴ `(square)/("EB") = ("AD")/("DC")` ....(II) (`square`)
∴ `("AB")/square = square/("EB")` [(I) व (II) से]
Chapter: [0.01] समरूपता
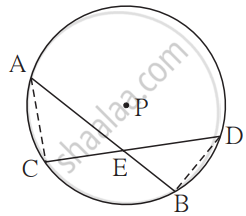
दत्त: वृत्त का केंद्र P है। जीवा AB और जीवा CD परस्पर बिंदु E पर प्रतिच्छेदित करती हैं।
साध्य: AE × EB = CE × ED
रचना: रेख AC और रेख DB खींचिए।
खाली जगह भरकर उपपत्ति पूर्ण कीजिए।
उपपत्ति: ΔCAE और ΔBDE में,
∠AEC ≅ ∠DEB ......... `square`
`square` ≅ ∠BDE .....(एक ही चाप में अंतर्लिखित कोण)
∴ ΔCAE ~ ΔBDE ........ `square`
∴ `square/ ("DE") = ("CE")/square` ........ `square`
∴ AE × EB = CE × ED
Chapter: [0.03] वृत्त
नीचे दिए गए बिंदु एकरेखीय हैं या नहीं? इसकी जाँच कीजिए।
A(1, −3), B(2, −5), C(−4, 7)
Chapter: [0.05] निर्देशांक भूमिति
ΔABC ~ ΔLMN , ΔABC में AB = 5.5 सेमी, BC = 6 सेमी, CA = 4.5 सेमी और `"BC"/"MN"` = `5/4` तो ΔABC तथा ΔLMN की रचना कीजिए।
Chapter: [0.04] भूमितीय रचनाएँ
ΔPQR में, रेख PM माध्यिका है PM = 9 और PQ2 + PR2 = 290 हो, तो QR ज्ञात कीजिए।
Chapter: [0.02] पाइथागोरस का प्रमेय
सिद्ध कीजिए “यदि किसी त्रिभुज की किसी एक भुजा के समांतर खींची गईं रेखा उसकी अन्य दो भुजाओं को दो भिन्न बिन्दुओं पर प्रतिच्छेदित करे तो वह रेखा अन्य दो भुजाओं को समान अनुपात में विभाजित करती है।
Chapter: [0.01] समरूपता
यदि `1/sin^2θ-1/cos^2θ-1/tan^2θ-1/cot^2θ-1/sec^2θ-1/("cosec"^2θ) = -3`, तो θ का मान ज्ञात कीजिए।
Chapter: [0.06] त्रिकोणमिति
किसी लंबवृत्ताकार बेलन की त्रिज्या 12 सेमी है जिसमें 20 सेमी ऊँचाई तक पानी भरा है। एक गोलाकार धातु की गेंद उसमें डुबाने पर पानी की ऊँचाई 6.75 सेमी कैसे बढ़ती है, तो उस धातु की गेंद की त्रिज्या ज्ञात कीजिए।
Chapter: [0.07] महत्वमापन
'O' केंद्र तथा 3 सेमी त्रिज्या का एक वृत्त बनाइए।वृत्त के बाहर स्थित बिंदु P से स्पर्श रेखाखंड PA तथा PB इस प्रकार बनाइये कि ∠APB = 70°
Chapter: [0.03] वृत्त
`square`ABCD एक समलंब चतुर्भुज है। AB || CD समलंब `square`ABCD के विकर्ण परस्पर बिंदु P में प्रतिच्छेदित करते हैं।
इस आधार पर नीचे दिए प्रश्नों के उत्तर लिखिए:
- दी गई जानकारी के आधार पर आकृति बनाइये।
- उस आधार पर एकांतर कोणों की तथा शीर्षाभिमुख कोणों की जोड़ियाँ लिखिए।
- समरूपता की कसौटीसह समरूप त्रिभुओं के नाम लिखिए।
Chapter: [0.01] समरूपता
‘O’ केंद्र वाले वृत्त की रेख AB जीवा है। AOC वृत्त का व्यास है। AT वृत्त के बिंदु A पर बनी स्पर्शरेखा है।
इस आधार पर नीचे दिए प्रश्नों के उत्तर लिखिए:
- दी गई जानकारी के आधार पर आकृति बनाइये।
- ∠CAT तथा ∠ABC की माप ज्ञात करने के लिए संबंधित प्रमेय का कथन लिखिए।
- क्या ∠CAT तथा ∠ABC एकरूप हैं? अपने उत्तर की पुष्टि कीजिये।
Chapter: [0.03] वृत्त
Other Solutions
Submit Question Paper
Help us maintain new question papers on Shaalaa.com, so we can continue to help studentsonly jpg, png and pdf files
Maharashtra State Board previous year question papers 10th Standard Board Exam [१० वीं कक्षा] Mathematics 2 - Geometry [गणित २ - ज्यामिति] with solutions 2023 - 2024
Previous year Question paper for Maharashtra State Board 10th Standard Board Exam [१० वीं कक्षा] -2024 is solved by experts. Solved question papers gives you the chance to check yourself after your mock test.
By referring the question paper Solutions for Mathematics 2 - Geometry [गणित २ - ज्यामिति], you can scale your preparation level and work on your weak areas. It will also help the candidates in developing the time-management skills. Practice makes perfect, and there is no better way to practice than to attempt previous year question paper solutions of Maharashtra State Board 10th Standard Board Exam [१० वीं कक्षा].
How Maharashtra State Board 10th Standard Board Exam [१० वीं कक्षा] Question Paper solutions Help Students ?
• Question paper solutions for Mathematics 2 - Geometry [गणित २ - ज्यामिति] will helps students to prepare for exam.
• Question paper with answer will boost students confidence in exam time and also give you an idea About the important questions and topics to be prepared for the board exam.
• For finding solution of question papers no need to refer so multiple sources like textbook or guides.
