Advertisements
Advertisements
Question
5 सेमी तथा 3 सेमी त्रिज्या वाले दो वृत्त परस्पर बाह्यस्पर्श करते हैं, तो उनके केंद्रों के बीच की दूरी ज्ञात कीजिए।
Solution
जब दो वृत्त एक दूसरे को बाह्य रूप से स्पर्श करते हैं, तो उनके केंद्रों के बीच की दूरी उनकी त्रिज्याओं के योग के बराबर होती है।
यह देखते हुए कि त्रिज्याएँ 5 सेमी और 3 सेमी हैं, उनके केंद्रों के बीच की दूरी है:
= 5 सेमी + 3 सेमी
= 8 सेमी
उनके केन्द्रों के बीच की दूरी 8 सेमी है।
APPEARS IN
RELATED QUESTIONS
परस्पर अंतःस्पर्श करनेवाले दो वृत्तों की त्रिज्याएँ क्रमशः 3.5 सेमी तथा 4.8 सेमी हों तो उनके केंद्रों के बीच की दूरी ज्ञात कीजिए।
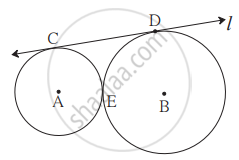
आकृति में A तथा B केंद्रवाले वृत्त परस्पर बिंदु E पर स्पर्श करते हैं। उनकी सामान्य स्पर्शरेखा l उन्हें क्रमशः C तथा D बिंदुओं पर स्पर्श करती है। यदि वृत्तों की त्रिज्या क्रमशः 4 सेमी तथा 6 सेमी हो तो रेख CD की लंबाई कितनी होगी?
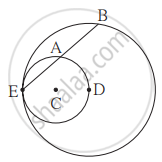
संलग्न आकृति में, C केंद्रवाला वृत्त D केंद्रवाले वृत्त को E बिंदु पर अंतःस्पर्श करता है। बिंदु D अंतःवृत्त पर है। बाह्य वृत्त की जीवा EB अंतःवृत्त को A बिंदु पर प्रतिच्छेदित करती है। सिद्ध कीजिए, कि रेख EA ≅ रेख AB
3 सेमी त्रिज्या तथा बिंदु A, B तथा C केंद्रवाले वृत्तों की रचना इस प्रकार कीजिए कि प्रत्येक वृत्त अन्य दो वृत्तों को स्पर्श करता हो।
आकृति में, N केंद्र वाला वृत्त M केंद्रवाले वृत्त को बिंदु T पर स्पर्श करता है । बड़े वृत्त की त्रिज्या छोटे वृत्त को बिंदु S पर स्पर्श करती है । यदि बड़े तथा छोटे वृत्तों की त्रिज्याएँ क्रमशः 9 सेमी तथा 2.5 सेमी हो तो निम्नलिखित प्रश्नों के उत्तर ज्ञात कर इसके आधार पर MS : SR का अनुपात ज्ञात कीजिए ।
(1) MT = कितना?
(2) MN = कितना?
(3) ∠NSM = कितना?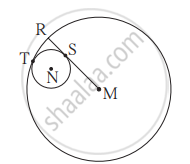
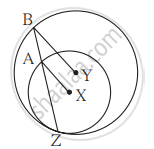
संलग्न आकृति में, X और Y केंद्रवाले वृत्त परस्पर Z बिंदु पर स्पर्श करते हैं | बिंदु Z से होकर जानेवाली वृत्त की छेदन रेखा उन वृत्तों को क्रमशः बिंदु A तथा बिंदु B पर प्रतिच्छेदित करती है | सिद्ध कीजिए कि त्रिज्या XA || त्रिज्या YB. नीचे दी गई उपपत्ति में रिक्त स्थानों की पूर्ति कर उपपत्ति को पूर्ण कीजिए ।
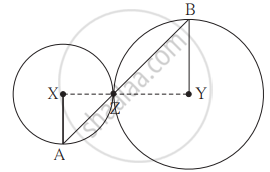
रचना: रेख XZ और ______ खींचिए ।
उपपत्ति:
स्पर्शवृत्तों के प्रमेयानुसार, बिंदु X, Z, Y ______ हैं ।
∴ ∠XZA ≅ ______ ...(शीर्षाभिमुख कोण)
माना ∠XZA = ∠BZY = a ...(I)
अब, रेख XA ≅ रेख XZ ...(______)
∴ ∠XAZ = ______ = a ....(समद्विबाहु त्रिभुज का प्रमेय) (II)
उसी प्रकार रेख YB ≅ ______ ...(______)
∴ ∠BZY = ______ = a ...(______) (III)
∴ (I), (II) तथा (III) से,
∠XAZ ≅ ______
∴ त्रिज्या XA || त्रिज्या YB ...(______)
आकृति में, बिंदु X तथा बिंदु Y केंद्रवाले अंतः स्पर्शी वृत्त बिंदु Z पर स्पर्श करते हैं। बड़े वृत्त की जीवा BZ छोटे वृत्त को बिंदु A पर प्रतिच्छेदित करती है, तो सिद्ध कीजिए, कि - रेख AX || रेख BY.
यदि ΔABC ∼ ΔDEF तथा ∠A = 48° हो, तो ∠D = ______.
