Advertisements
Advertisements
Question
सिद्ध कीजिए “यदि किसी त्रिभुज की किसी एक भुजा के समांतर खींची गईं रेखा उसकी अन्य दो भुजाओं को दो भिन्न बिन्दुओं पर प्रतिच्छेदित करे तो वह रेखा अन्य दो भुजाओं को समान अनुपात में विभाजित करती है।
Solution
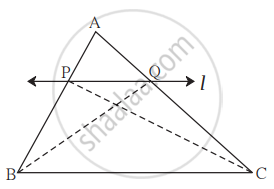
दत्त: ΔABC में रेखा l || भुजा BC और रेखा l यह भुजा AB को बिंदु P पर तथा भुजा AC को बिंदु Q पर प्रतिच्छेदित करती है।
साध्य: `(AP)/(PB) = (AQ)/(QC)`
रचन: रेख PC तथा रेख BQ खींचिए।
उपपत्ति: ΔAPQ तथा ΔPQB समान ऊँचाई वाले त्रिभुज हैं।
∴ `(A(ΔAPQ))/(A (ΔPQB)) = (AP)/(PB)` ...(आधार के अनुपात में क्षेत्रफल) ...(I)
इसी प्रकार `(A(ΔAPQ))/(A (ΔPQC)) = (AQ)/(QC)` ...(आधार के अनुपात में क्षेत्रफल) ... (II)
ΔPQB तथा ΔPQC में रेख PQ सामान्य आधार है ।रेख PQ || रेख BC इसलिए ΔPQB तथा ΔPQC की ऊँचाई समान है।
A (ΔPQB) = A(ΔPQC) ....(III)
∴ `(A(ΔAPQ))/(A (ΔPQB)) = (A(APQ))/(A(PQC))` ...[(I), (II) तथा (III)] से
∴`(AP)/(PB) = (AQ)/(QC)` ...[(I) तथ (II)] से
APPEARS IN
RELATED QUESTIONS
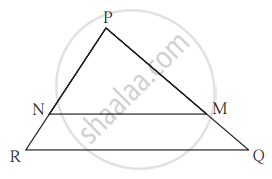
ΔPQR में PM = 15, PQ = 25, PR = 20, NR = 8 तो बताइए रेख NM भुजा RQ के समांतर है क्या? कारण लिखिए।
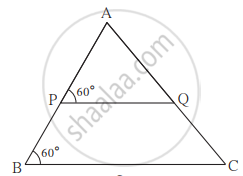
आकृति में कुछ कोणों के माप दिए गए हैं। इनके आधार पर सिद्ध कीजिए कि, `"AP"/"PB" = "AQ"/"QC"`
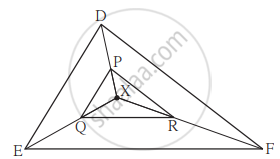
संलग्न आकृति में त्रिभुज के अंत:भाग में स्थित एक बिंदु X है। बिंदु X को त्रिभुज के शीर्षबिंदुओं से जोड़ा गया है। इसी प्रकार रेख PQ || रेख DE, रेख QR || रेख EF, तो रेख PR || रेख DF को सिद्ध करने के लिए निम्नलिखित चौखटों को पूरा कीजिए।
उपपत्ति : ΔXDE में PQ || DE ..........`square`
∴ `"XP"/square = square/"QE"` .............(I) (समानुपात का मूलभूत प्रमेय)
ΔXEF में QR || EF ..........`square`
∴ `square/square = square/square` .........(II) `square`
∴ `square/square = square/square` ..............कथन (I) तथा (II) से
∴ रेख PR || रेख DF ............. (समानुपात के मूलभूत प्रमेय का विलोम)
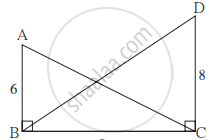
आकृति में ∠ABC = ∠DCB = 90° AB = 6, DC = 8 तो `("A"(Δ"ABC"))/("A"(Δ"DCB"))` = कितना?
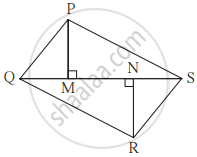
आकृति में PM = 10 सेमी A(ΔPQS) = 100 वर्ग सेमी, A(ΔQRS) = 110 वर्ग सेमी तो NR का मान ज्ञात कीजिए।
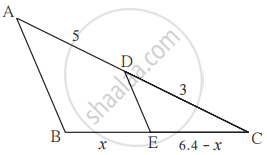
आकृति में A – D – C व B – E – C रेख DE || भुजा AB यदि AD = 5, DC = 3, BC = 6.4 तो BE का मान ज्ञात कीजिए।