Advertisements
Advertisements
Question
किसी द्वैत्रिज्य की त्रिज्या 3.5 सेमी तथा उसके वृत्त चाप की लंबाई 2.2 सेमी हो तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
Solution
द्वैत्रिज्य की त्रिज्या (r) = 3.5 सेमी
चाप की लंबाई = 2.2 सेमी
द्वैत्रिज्य का क्षेत्रफल = `("वृत्त चाप की लंबाई" xx "त्रिज्या")/2`
= `(2.2 xx 3.5)/2` = 3.85 सेमी2
द्वैत्रिज्य का क्षेत्रफल 3.85 सेमी2 है |
RELATED QUESTIONS
किसी वृत्त की त्रिज्या 10 सेमी तथा वृत्त चाप का माप 54° हो तो उस चाप द्वारा सीमित द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए। (π =3.14)
किसी वृत्त की त्रिज्या 10 सेमी तथा उसके लघु द्वैत्रिज्य का क्षेत्रफल 100 वर्ग सेमी हो तो उसके दीर्घ द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए। (π = 3.14)
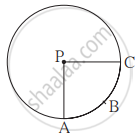
संलग्न आकृति में, 3.4 सेमी त्रिज्यावाले द्वैत्रिज्य P-ABC की परिमिति 12.8 सेमी है तो द्वैत्रिज्य P-ABC का क्षेत्रफल ज्ञात कीजिए।

संलग्न आकृति में A(P-ABC) = 154 वर्ग सेमी और वृत्त की त्रिज्या 14 सेमी हो, तो
(1) ∠APC का माप ज्ञात कीजिए।
(2) चाप ABC की लंबाई ज्ञात कीजिए।
किसी द्वैत्रिज्य की त्रिज्या 7 सेमी है। यदि द्वैत्रिज्य के चाप का माप निम्नलिखित है तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
30°
किसी द्वैत्रिज्य की त्रिज्या 7 सेमी है। यदि द्वैत्रिज्य के चाप का माप निम्नलिखित है तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
210°
किसी द्वैत्रिज्य की त्रिज्या 7 सेमी है। यदि द्वैत्रिज्य के चाप का माप निम्नलिखित है तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
3 समकोण
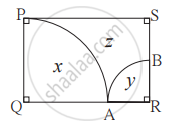
संलग्न आकृति में `square`PQRS एक आयत है। PQ = 14 सेमी, QR = 21 सेमी, हो तो आकृति में दर्शाएनुसार x, y और z इस प्रत्येक भाग का क्षेत्रफल ज्ञात कीजिए।
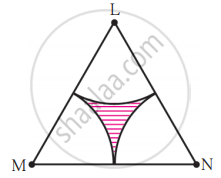
ΔLMN समबाहु त्रिभुज है। LM = 14 सेमी. त्रिभुज के प्रत्येक शीर्ष बिंदु को केंद्र मानकर तथा 7 सेमी त्रिज्या लेकर आकृति में दर्शाएनुसार तीन द्वैत्रिज्य खींचकर उसके आधार पर,
(1) A (ΔLMN) = ?
(2) एक द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
(3) तीनों द्वैत्रिज्यों का संपूर्ण क्षेत्रफल ज्ञात कीजिए।
(4) रेखांकित भाग का क्षेत्रफल ज्ञात कीजिए।
द्वैत्रिज्य A-PCQ में `square`ABCD यह एक वर्ग है। द्वैत्रिज्य C - BXD की त्रिज्या 20 सेमी हो तो छायांकित भाग का क्षेत्रफल ज्ञात करने के लिए नीचे दी गई कृति पूर्ण कीजिए।
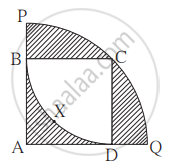
हल : वर्ग ABCD की भुजा = द्वैत्रिज्य C - BXD की त्रिज्या = `square` सेमी
वर्ग का क्षेत्रफल = (भुजा)2 = `square^2 = square` ............(I)
वर्ग के छायांकित भाग का क्षेत्रफल
= वर्ग ABCD का क्षेत्रफल - द्वैत्रिज्य C - BXD का क्षेत्रफल
= `square - theta/360 xx pir^2`
= `square - 90/360 xx 3.14/1 xx 400/1`
= `square - 314`
= `square`
बड़े द्वैत्रिज्य की त्रिज्या = वर्ग ABCD के विकर्ण की लंबाई
= `20sqrt2`
बड़े द्वैत्रिज्य में वर्ग के बाहर के छायांकित भाग का क्षेत्रफल
= द्वैत्रिज्य (A - PCQ) का क्षेत्रफल - वर्ग ABCD का क्षेत्रफल
= A(A - PCQ) - A(`square` ABCD)
= `(theta/360 xx pi xx r^2) - square^2`
= `90/360 xx 3.14(20sqrt2)^2 - (20)^2`
= `square - square`
= `square`
∴ छायांकित भाग का संपूर्ण क्षेत्रफल = 86 + 228 = 314 वसेमी
