Advertisements
Advertisements
Question
द्वैत्रिज्य A-PCQ में `square`ABCD यह एक वर्ग है। द्वैत्रिज्य C - BXD की त्रिज्या 20 सेमी हो तो छायांकित भाग का क्षेत्रफल ज्ञात करने के लिए नीचे दी गई कृति पूर्ण कीजिए।
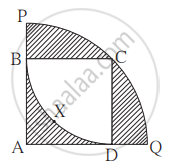
हल : वर्ग ABCD की भुजा = द्वैत्रिज्य C - BXD की त्रिज्या = `square` सेमी
वर्ग का क्षेत्रफल = (भुजा)2 = `square^2 = square` ............(I)
वर्ग के छायांकित भाग का क्षेत्रफल
= वर्ग ABCD का क्षेत्रफल - द्वैत्रिज्य C - BXD का क्षेत्रफल
= `square - theta/360 xx pir^2`
= `square - 90/360 xx 3.14/1 xx 400/1`
= `square - 314`
= `square`
बड़े द्वैत्रिज्य की त्रिज्या = वर्ग ABCD के विकर्ण की लंबाई
= `20sqrt2`
बड़े द्वैत्रिज्य में वर्ग के बाहर के छायांकित भाग का क्षेत्रफल
= द्वैत्रिज्य (A - PCQ) का क्षेत्रफल - वर्ग ABCD का क्षेत्रफल
= A(A - PCQ) - A(`square` ABCD)
= `(theta/360 xx pi xx r^2) - square^2`
= `90/360 xx 3.14(20sqrt2)^2 - (20)^2`
= `square - square`
= `square`
∴ छायांकित भाग का संपूर्ण क्षेत्रफल = 86 + 228 = 314 वसेमी
Solution
वर्ग ABCD की भुजा = द्वैत्रिज्य C - BXD की त्रिज्या = 20 सेमी
वर्ग का क्षेत्रफल = (भुजा)2 = 202 = 400 सेमी2 ............(I)
वर्ग के छायांकित भाग का क्षेत्रफल
= वर्ग ABCD का क्षेत्रफल - द्वैत्रिज्य C - BXD का क्षेत्रफल
= `underline400 - theta/360 xx pir^2`
= `underline400 - 90/360 xx 3.14/1 xx 400/1`
= `underline400 - 314`
= 86 सेमी2
बड़े द्वैत्रिज्य की त्रिज्या = वर्ग ABCD के विकर्ण की लंबाई
= `20sqrt2`
बड़े द्वैत्रिज्य में वर्ग के बाहर के छायांकित भाग का क्षेत्रफल
= द्वैत्रिज्य (A - PCQ) का क्षेत्रफल - वर्ग ABCD का क्षेत्रफल
= A(A - PCQ) - A(`square` ABCD)
= `(theta/360 xx pi xx r^2) - underline(20^2)`
= `90/360 xx 3.14(20sqrt2)^2 - (20)^2`
= 628 - 400
= 228 सेमी2
∴ छायांकित भाग का संपूर्ण क्षेत्रफल = 86 + 228 = 314 सेमी2
APPEARS IN
RELATED QUESTIONS
किसी वृत्त की त्रिज्या 10 सेमी तथा वृत्त चाप का माप 54° हो तो उस चाप द्वारा सीमित द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए। (π =3.14)
किसी द्वैत्रिज्य की त्रिज्या 3.5 सेमी तथा उसके वृत्त चाप की लंबाई 2.2 सेमी हो तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
किसी वृत्त की त्रिज्या 10 सेमी तथा उसके लघु द्वैत्रिज्य का क्षेत्रफल 100 वर्ग सेमी हो तो उसके दीर्घ द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए। (π = 3.14)
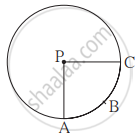
संलग्न आकृति में, 3.4 सेमी त्रिज्यावाले द्वैत्रिज्य P-ABC की परिमिति 12.8 सेमी है तो द्वैत्रिज्य P-ABC का क्षेत्रफल ज्ञात कीजिए।

संलग्न आकृति में A(P-ABC) = 154 वर्ग सेमी और वृत्त की त्रिज्या 14 सेमी हो, तो
(1) ∠APC का माप ज्ञात कीजिए।
(2) चाप ABC की लंबाई ज्ञात कीजिए।
किसी द्वैत्रिज्य की त्रिज्या 7 सेमी है। यदि द्वैत्रिज्य के चाप का माप निम्नलिखित है तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
30°
किसी द्वैत्रिज्य की त्रिज्या 7 सेमी है। यदि द्वैत्रिज्य के चाप का माप निम्नलिखित है तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
210°
किसी द्वैत्रिज्य की त्रिज्या 7 सेमी है। यदि द्वैत्रिज्य के चाप का माप निम्नलिखित है तो द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
3 समकोण
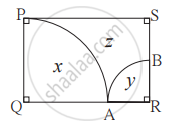
संलग्न आकृति में `square`PQRS एक आयत है। PQ = 14 सेमी, QR = 21 सेमी, हो तो आकृति में दर्शाएनुसार x, y और z इस प्रत्येक भाग का क्षेत्रफल ज्ञात कीजिए।
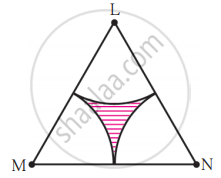
ΔLMN समबाहु त्रिभुज है। LM = 14 सेमी. त्रिभुज के प्रत्येक शीर्ष बिंदु को केंद्र मानकर तथा 7 सेमी त्रिज्या लेकर आकृति में दर्शाएनुसार तीन द्वैत्रिज्य खींचकर उसके आधार पर,
(1) A (ΔLMN) = ?
(2) एक द्वैत्रिज्य का क्षेत्रफल ज्ञात कीजिए।
(3) तीनों द्वैत्रिज्यों का संपूर्ण क्षेत्रफल ज्ञात कीजिए।
(4) रेखांकित भाग का क्षेत्रफल ज्ञात कीजिए।